
【题目】有理数a、b、c在数轴上的位置如图所示
![]()
(1)比较a、b、|c|的大小(用“>”连接);
(2)若n=|b+c|﹣|c﹣1|﹣|b﹣a|,求![]() 的值;
的值;
(3)若a=![]() ,b=﹣2,c=﹣3,且a、b、c对应的点分别为A、B、C,问在数轴上是否存在一点M,使M与B的距离是M与A的距离的3倍,若存在,请求出M点对应的有理数;若不存在,请说明理由.
,b=﹣2,c=﹣3,且a、b、c对应的点分别为A、B、C,问在数轴上是否存在一点M,使M与B的距离是M与A的距离的3倍,若存在,请求出M点对应的有理数;若不存在,请说明理由.
【答案】(1)![]() ;(2)-2016;(3)点M对应的数是
;(2)-2016;(3)点M对应的数是![]() 或
或![]()
【解析】
(1)根据数轴得到c<b<-1<0<a<1,![]() ,即可得到答案;
,即可得到答案;
(2)先确定![]() ,c-1<0,b-a<0,再化简绝对值得到n+a=-1,再代入计算即可;
,c-1<0,b-a<0,再化简绝对值得到n+a=-1,再代入计算即可;
(3)设点M对应的数是x,根据MB=3MA列方程求解即可.
(1)由数轴知:c<b<-1<0<a<1,
∴ ![]() ,
,
∴![]() ;
;
(2)∵c<b<-1<0<a<1,
∴![]() ,c-1<0,b-a<0,
,c-1<0,b-a<0,
∴n=|b+c|﹣|c﹣1|﹣|b﹣a|=-b-c+c-1+b-a=-1-a,
∴n+a=-1,
∴1-2017![]() ;
;
(3)存在,
设点M对应的数是x,
①当但M在AB之间时,此时BM=x+2,AM=![]() -x,
-x,
∵BM=3AM,
∴x+2=3(![]() -x),
-x),
![]() ;
;
②当点M在AB左侧时,BM=-2-x,AM=![]() -x,
-x,
∵BM=3AM,
∴-2-x=3(![]() -x),
-x),
![]() ,与点M对应的数是负数相矛盾,故舍去;
,与点M对应的数是负数相矛盾,故舍去;
③当点M在AB右侧时,BM=x+2,AM=x-![]() ,
,
∵BM=3AM,
∴x+2=3(x-![]() ),
),
![]() ,
,
综上,点M对应的数是![]() 或
或![]() .
.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是☉O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() =
=![]() ,连接AF并延长交☉O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=3;③tan∠E=
,连接AF并延长交☉O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=3;③tan∠E=![]() ;④S△ADF=6
;④S△ADF=6![]() .
.
其中正确结论的个数是( )
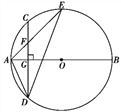
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保持水土,美化环境,W中学准备在从校门口到柏油公路的这一段土路的两侧栽一些树,并要求土路两侧树的棵数相等间距也相等,且首、尾两端均栽上树,现在学校已备好一批树苗,若间隔30米栽一棵,则缺少22棵;若间隔35米栽一棵,则缺少14棵
(1)求学校备好的树苗棵数.
(2)某苗圃负责人听说W中学想在校外土路两旁栽树的上述情况后,觉得两树间距太大,既不美观,又影响防风固沙的效果,决定无偿支援W中学300棵树苗.请问,这些树苗加上学校自己备好的树苗,间隔5米栽一棵,是否够用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长为( )
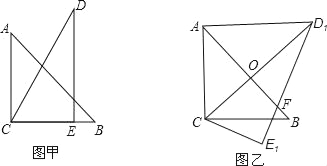
A. ![]() B. 5 C. 4 D.
B. 5 C. 4 D. ![]()
【答案】B
【解析】由旋转的性质可知,在图乙中,∠BCE1=15°,∠D1CE1=60°,AB=6,CD1=CD=7,
∴∠D1CB=60°-15°=45°,
又∵∠ACB=90°,
∴CO平分∠ACB,
又∵AC=BC,
∴CO⊥AB,且CO=AO=BO=![]() AB=3,
AB=3,
∴D1O=CD1-CO=7-3=4,∠AOD1=90°,
∴在Rt△AOD1中,AD1=![]() .
.
故选B.
点睛:本题解题的关键是由旋转的性质证明:∠D1CB=45°,从而得到CD1平分∠ACB,结合等腰三角形的“三线合一”证得∠AOD1=90°,并求得AO=3,OD1=4;这样问题就变得很简单了.
【题型】单选题
【结束】
10
【题目】我市某小区实施供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中,正确的个数有( )个.
①甲队每天挖100米;
②乙队开挖两天后,每天挖50米;
③当x=4时,甲、乙两队所挖管道长度相同;
④甲队比乙队提前2天完成任务.
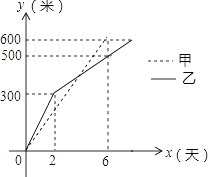
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题:

(1)机动车行驶几小时后加油?加了多少油?
(2)请求出加油前油箱余油量Q与行驶时间t之间的关系式;
(3)如果加油站离目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样规格的黑白两种颜色的正方形,按如图的方式拼图,请根据图中的信息完成下列的问题.

(1)在图②中用了 块黑色正方形,在图③中用了 块黑色正方形;
(2)按如图的规律继续铺下去,那么第![]() 个图形要用 块黑色正方形;
个图形要用 块黑色正方形;
(3)如果有足够多的白色正方形,能不能恰好用完90块黑色正方形,拼出具有以上规律的图形?如果可以请说明它是第几个图形;如果不能,说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=4,AC=6,点D、E分别是BC.AD的中点,AF∥BC交CE的延长线于F.则四边形AFBD的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
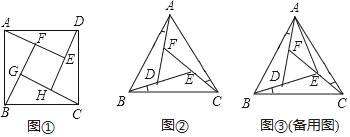
【题目】【问题背景】
如图①所示,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.
【类比研究】
如图②所示,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合).
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)连结AE,若AF=DF,AB=7,求△DEF的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南方某地突降暴雨,造成山洪爆发,导致一条重要公路损毁严重,某部工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的![]() 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
(1)按原计划完成总任务的![]() 时,已抢修道路 米;
时,已抢修道路 米;
(2)求原计划每小时抢修道路多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com