
科目:初中数学 来源: 题型:选择题
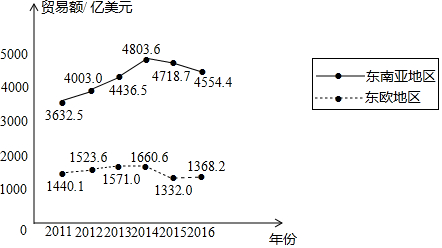
| A. | 与2015年相比,2016年我国与东欧地区的贸易额有所增长 | |
| B. | 2011-2016年,我国与东南亚地区的贸易额逐年增长 | |
| C. | 2011-2016年,我国与东南亚地区的贸易额的平均值超过4200亿美元 | |
| D. | 2016年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的3倍还多 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
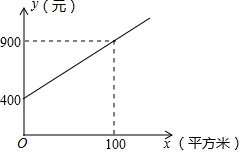 甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C作CF∥AB,与过点B的切线交于点F,连接BD.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C作CF∥AB,与过点B的切线交于点F,连接BD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>-1 | B. | x<3 | C. | x<-1或x>3 | D. | -1<x<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
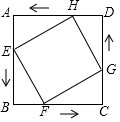 如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为3s时,四边形EFGH的面积最小,其最小值是18cm2.
如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为3s时,四边形EFGH的面积最小,其最小值是18cm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
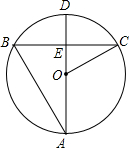 如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC的长为( )
如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC的长为( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com