
【题目】如图所示,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,以
上,以![]() 为直径的
为直径的![]() 与
与![]() 相交于点
相交于点![]() ,与
,与![]() 相交于点
相交于点![]() ,
,![]() 平分
平分![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求图中阴影部分的面积;
,求图中阴影部分的面积;
(3)若![]() ,
,![]() ,求
,求![]() .
.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据角平分线的定义得到∠CAE=∠EAD,根据等腰三角形的性质得到∠EAD=∠OEA根据平行线的性质得到∠OEB=∠C=90°,于是得到结论;
(2)根据勾股定理得到BE=![]() ,根据图形的面积即可得到结论;
,根据图形的面积即可得到结论;
(3)连结DE,根据勾股定理求出DE长,证明△ACE∽△AED,求出AC,CE长,连结EF,证明△CEF∽△CAE,由比例线段可求出CF长,则AF的长可求出.
(1)证明:如图所示,连接![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的切线;
的切线;
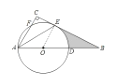
(2)解:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
(3)如图所示,连接![]() ,
,![]() ,
,
![]() 为
为![]() 的直径,
的直径,
![]() ,
,
![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 为圆内接四边形,
为圆内接四边形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
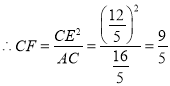 ,
,
![]() .
.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴的一个交点为
轴的一个交点为![]() ,另一个交点为
,另一个交点为![]() ,且与
,且与![]() 轴相交于
轴相交于![]() 点
点
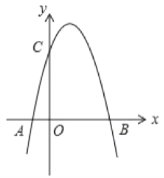
(1)则![]() _________;
_________;![]() 点坐标为___________;
点坐标为___________;
(2)在直线![]() 上方的抛物线上是否存在一点
上方的抛物线上是否存在一点![]() ,使得它与
,使得它与![]() ,
,![]() 两点构成的三角形面积最大,若存在,求出此时
两点构成的三角形面积最大,若存在,求出此时![]() 点坐标;若不存在,请简要说明理由.
点坐标;若不存在,请简要说明理由.
(3)![]() 为抛物线上一点,它关于直线
为抛物线上一点,它关于直线![]() 的对称点为
的对称点为![]()
①当四边形![]() 为菱形时,求点
为菱形时,求点![]() 的坐标;
的坐标;
②点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() ________时,四边形
________时,四边形![]() 的面积最大.
的面积最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
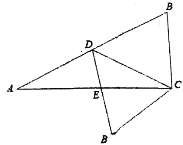
【题目】已知Rt△ABC,∠ACB=90,BC=10,AC=20,点D为斜边中点,连接CD,将△BCD沿CD翻折得△B’CD,B’D交AC于点E,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古贤常说万物皆自然,而古希腊学者说万物皆数.同学们还记得我们最初接触的数就是“自然数”吧!在数的学习过程中,我们会对其中一些具有某种特性的自然数进行研究,我们研究了奇数、偶数、质数、合数等.现在我们来研究另一种特珠的自然数—“![]() 喜数”.
喜数”.
定义:对于一个两位自然数,如果它的个位和十位上的数字均不为零,且它正好等于其个位和十位上的数字的和的![]() 倍(
倍(![]() 为正整数),我们就说这个自然数是一个“
为正整数),我们就说这个自然数是一个“![]() 喜数”.
喜数”.
例如:24就是一个“4喜数”,因为![]()
25就不是一个“![]() 喜数”因为
喜数”因为![]()
(1)判断44和72是否是“![]() 喜数”?请说明理由;
喜数”?请说明理由;
(2)试讨论是否存在“7喜数”若存在请写出来,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
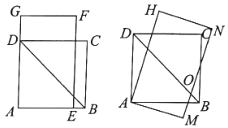
【题目】如图所示,四边形![]() 是边长为
是边长为![]() 的正方形,长方形
的正方形,长方形![]() 的宽
的宽![]() ,长
,长![]() .将长方形
.将长方形![]() 绕点
绕点![]() 顺时针旋转15°得到长方形
顺时针旋转15°得到长方形![]() (如图所示),这时
(如图所示),这时![]() 与
与![]() 相交于点
相交于点![]() .则在图中,
.则在图中,![]() ,
,![]() 两点间的距离是( )
两点间的距离是( )
A.![]() B.5C.
B.5C.![]() D.7
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
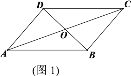
【题目】我们把有两边对应相等,且夹角互补(不相等)的两个三角形叫做“互补三角形”,如图1,□ABCD中,△AOB和△BOC是“互补三角形”.
(1)写出图1中另外一组“互补三角形”_______;
(2)在图2中,用尺规作出一个△EFH,使得△EFH和△EFG为“互补三角形”,且△EFH和△EFG在EF同侧,并证明这一组“互补三角形”的面积相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E、F在四边形ABCD的对角线延长线上,AE=CF,DE∥BF,∠1=∠2.
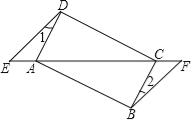
(1)求证:△AED≌△CFB;
(2)若AD⊥CD,四边形ABCD是什么特殊四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
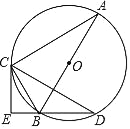
【题目】如图,AB为⊙O直径,C、D为⊙O上的点,∠ACD=2∠A,CE⊥DB交DB的延长线于点E.
(1)求证:直线CE与⊙O相切;
(2)若AC=8,AB=10,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有2个白球、1个红球、1个黄球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好是白球的概率是 ;
(2)从中任意摸出2个球,求2个球都是白球的概率(用画树状图或列表等方法求解).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com