【题目】一只不透明的袋子中装有2个白球、1个红球、1个黄球，这些球除颜色外都相同，将球搅匀．
（1）从中任意摸出1个球，恰好是白球的概率是 ；
（2）从中任意摸出2个球，求2个球都是白球的概率（用画树状图或列表等方法求解）．
科目：初中数学 来源： 题型：
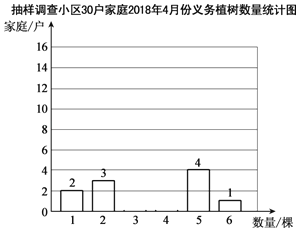
【题目】“绿水青山就是金山银山”，北京市民积极参与义务植树活动．小武同学为了了解自己小区300户家庭在2018年4月份义务植树的数量，进行了抽样调查，随即抽取了其中30户家庭，收集的数据如下（单位：棵）：
1 1 2 3 2 3 2 3 3 4 3 3 4 3 3
5 3 4 3 4 4 5 4 5 3 4 3 4 5 6
（1）对以上数据进行整理、描述和
①绘制如下的统计图，请补充完整；
②这30户家庭2018年4月份义务植树数量的平均数是______，众数是______；
（2）“互联网＋全民义务植树”是新时代首都全民义务植树组织形式和尽责方式的一大创新，2018年首次推出义务植树网上预约服务，小武同学所调查的这30户家庭中有7户家庭采用了网上预约义务植树这种方式，由此可以估计该小区采用这种形式的家庭有______户．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB为⊙O的直径，点C为
下方的一动点，连结OC，过点O作OD⊥OC交BC于点D，过点C作AB的垂线，垂足为F，交DO的延长线于点E．
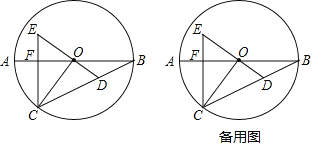
（1）求证：EC＝ED．
（2）当OE＝OD，AB＝4时，求OE的长．
（3）设
＝x，tanB＝y．
①求y关于x的函数表达式；
②若△COD的面积是△BOD的面积的3倍，求y的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
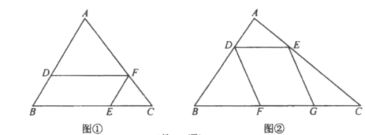
【题目】如图①，在
中，点
分别在
上，且
．设
的边
上的高为
，
的边
上的高为
．
（1）若、的面积分别为3，1，则
；
（2）设、、四边形
的面积分别为
，求证：
；
（3）如图②，在中，点
分别在
上，点
在
上，且
， 
． 若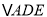
、
、
的面积分别为3， 7， 5，求的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公司推出一款产品，经市场调查发现，该产品的日销售量y（个）与销售单价x（元）之间满足一次函数关系．关于销售单价，日销售量，日销售利润的几组对应值如下表：
销售单价x（元） | 85 | 95 | 105 | 115 |
日销售量y（个） | 175 | 125 | 75 | m |
日销售利润w（元） | 875 | 1875 | 1875 | 875 |
（注：日销售利润=日销售量×（销售单价﹣成本单价））
（1）求y关于x的函数解析式（不要求写出x的取值范围）及m的值；
（2）根据以上信息，填空：
该产品的成本单价是 元，当销售单价x= 元时，日销售利润w最大，最大值是 元；
（3）公司计划开展科技创新，以降低该产品的成本，预计在今后的销售中，日销售量与销售单价仍存在（1）中的关系．若想实现销售单价为90元时，日销售利润不低于3750元的销售目标，该产品的成本单价应不超过多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
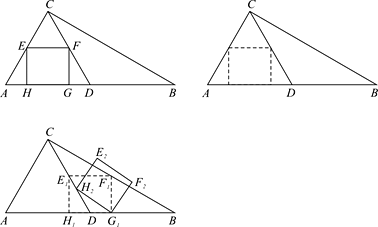
【题目】如图①，在△ABC中，∠ACB=90°，∠B=30°，AC=1，D为AB的中点，EF为△ACD 的中位线，四边形EFGH为△ACD的内接矩形（矩形的四个顶点均在△ACD的边上）．
（1）计算矩形EFGH的面积；
（2）将矩形EFGH沿AB向右平移，F落在BC上时停止移动．在平移过程中，当矩形与△CBD重叠部分的面积为
时，求矩形平移的距离；
（3）如图③，将（2）中矩形平移停止时所得的矩形记为矩形
，将矩形绕
点按顺时针方向旋转，当
落在CD上时停止转动，旋转后的矩形记为矩形
，设旋转角为
，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线
过点A（﹣3，0），B（﹣2，3），C（0，3），其顶点为D．
（1）求抛物线的解析式；
（2）设点M（1，m），当MB+MD的值最小时，求m的值；
（3）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值；
（4）若抛物线的对称轴与直线AC相交于点N，E为直线AC上任意一点，过点E作EF∥ND交抛物线于点F，以N，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
