
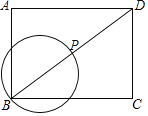
【题目】如图,在矩形ABCD中,AB=3,BC=4,P是对角线BD上的动点,以BP为直径作圆,当圆与矩形ABCD的边相切时,BP的长为__.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】中国古贤常说万物皆自然,而古希腊学者说万物皆数.同学们还记得我们最初接触的数就是“自然数”吧!在数的学习过程中,我们会对其中一些具有某种特性的自然数进行研究,我们研究了奇数、偶数、质数、合数等.现在我们来研究另一种特珠的自然数—“![]() 喜数”.
喜数”.
定义:对于一个两位自然数,如果它的个位和十位上的数字均不为零,且它正好等于其个位和十位上的数字的和的![]() 倍(
倍(![]() 为正整数),我们就说这个自然数是一个“
为正整数),我们就说这个自然数是一个“![]() 喜数”.
喜数”.
例如:24就是一个“4喜数”,因为![]()
25就不是一个“![]() 喜数”因为
喜数”因为![]()
(1)判断44和72是否是“![]() 喜数”?请说明理由;
喜数”?请说明理由;
(2)试讨论是否存在“7喜数”若存在请写出来,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
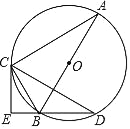
【题目】如图,AB为⊙O直径,C、D为⊙O上的点,∠ACD=2∠A,CE⊥DB交DB的延长线于点E.
(1)求证:直线CE与⊙O相切;
(2)若AC=8,AB=10,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x<3时,y1<y2;④当y1>0且y2>0时,﹣a<x<4.其中正确的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,且AB=6.点C是⊙O上的一动点,连接AC,BC,在AC的延长线上取一点D,使得∠CBD=∠DAB,点G为DB的中点,点E为BG的中点,连接AE交BC于点F.
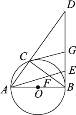
(1)试判断直线BD与⊙O的位置关系,并说明理由;
(2)当∠CGB=60°时,求![]() 的长;
的长;
(3)当AE∥CG时,连接GF,若AF=4,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研制了新产品1520kg,为寻求合适的销售价格,进行了8天试销,共销售470kg.统计发现每天的销售量y(千克)与销售价格x(元/千克)之间满足函数关系y=﹣x+120.
(1)在试销8天后,公司决定将这种产品的销售价格定为50元/千克,并且每天都按这个价格销售,则余下的产品再用多少天全部售完?
(2)在(1)的条件下,公司继续销售9天后,发现剩余的产品必须在5天内全部售完,此时需要重新确定一个销售价格,使后面都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有2个白球、1个红球、1个黄球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好是白球的概率是 ;
(2)从中任意摸出2个球,求2个球都是白球的概率(用画树状图或列表等方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
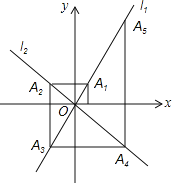
【题目】如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过A1点作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2019的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com