
����Ŀ��ij��˾�������²�Ʒ1520kg��ΪѰ����ʵ����ۼ۸�����8��������������470kg��ͳ�Ʒ���ÿ���������y��ǧ�ˣ������ۼ۸�x��Ԫ/ǧ�ˣ�֮�����㺯����ϵy����x+120��
��1��������8���˾���������ֲ�Ʒ�����ۼ۸�Ϊ50Ԫ/ǧ�ˣ�����ÿ�춼������۸����ۣ������µIJ�Ʒ���ö�����ȫ�����ꣿ
��2���ڣ�1���������£���˾��������9�����ʣ��IJ�Ʒ������5����ȫ�����꣬��ʱ��Ҫ����ȷ��һ�����ۼ۸�ʹ���涼���µļ۸����ۣ���ô��ȷ���ļ۸���߲�����ÿǧ�˶���Ԫ���������������
���𰸡���1��ʣ��IJ�Ʒ��Ҫ�����ʱ��Ϊ15�죻��2���¼۸���߲�����ÿǧ��38Ԫ���������������
��������
��1�������ۼ۸�Ϊ50Ԫ/ǧ��ʱ������ÿ���������y��ǧ�ˣ������ۼ۸�x��Ԫ/ǧ�ˣ�֮��Ĺ�ϵʽ���ÿ�����������Ȼ����ÿ��������������ۼ۸ɽ��
ÿ�������y=-50+ 120=70��������⣻
��2������˾��������9������ʣ��IJ�Ʒ����Ϊ410��Ȼ��������ã�5y��410�����ɽ��
�⣺��1�����ۼ۸�Ϊ50Ԫ/ǧ��ʱ��ÿ�����������y����x+120����50+120��70��
��ʣ��IJ�Ʒ��Ҫ�����ʱ��Ϊ��![]() ��15��
��15��
��2����˾��������9���ʣ��IJ�Ʒ����Ϊ��1520��470��9��70��410��
���¼۸�ΪxԪ��������ã�5y��410��
��5����x+120����410��
��ã�x��38��
���¼۸���߲�����ÿǧ��38Ԫ���������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����![]() �У�
��![]() ��
��![]() �����ģ�
�����ģ�![]() �����ģ���
�����ģ���![]() ���ڣ� )
���ڣ� )

A.130��B.135��C.140��D.145��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������й�����70����֮�ʣ�ijУ��չ����У�Ļ�������������Ŀ�У��鷨���滭�����ֺ����֣�Ҫ��ȫУѧ�����˲μӣ�����ÿ��ֻ�ܲμ�����һ�������̴��ڸ�Уѧ���������ȡ��100��ѧ�����е����ͳ�ƣ�������������������������ͳ��ͼ������ͼ��������ݽ���������⣺
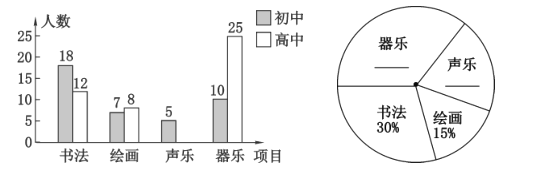
��1���벹ȫ����ͳ��ͼ������ͳ��ͼ��
��2����У����ѧ���У��μ����鷨����Ŀ��ѧ����ռ�İٷֱ��Ƕ��٣�
��3������У����1500�ˣ���������вμ�����������Ŀ�ĸ���ѧ���ж����ˣ�
��4�������̴������вμ����滭����Ŀ����Ʒ�������ȣ���ѡ��2������ѧ����2������ѧ���������Ʒ��ѧУ��������4��ѧ���������ȡ2����Ϊѧ�������滭����������������ô���ó鵽һ������ѧ����һ������ѧ���ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������̳��ﹺ���ܺ���90Ԫ����Ʒ�ס��ҡ��������Σ����мĵ�����20Ԫ���ҵĵ�����40Ԫ������Ʒ��һ�ι���������ǵڶ��ι�������������������Ʒ��һ�ι�������������Ʒ�ڶ��ι����������ȣ����ι�����Ʒ�ס��ҡ������������ܷ������±���
������Ʒ�� ����(��) | ������Ʒ�ҵ� ����(��) | ������Ʒ���� ����(��) | �����ܷ���(Ԫ) | |
��һ�ι��� | 4 | 440 | ||
�ڶ��ι��� | 7 | 490 |
(1)�����ι���ס��ҡ���������Ʒ���������ֱ��Ƕ��٣�
(2)���������̳�������������������������ǰ��������Ʒ�ס��ҡ�������������Ʒ�������ܺ�Ϊa�������й�������Ʒ�����Ǽ���Ʒ������3���������ܷ���Ϊ1 280Ԫ����a����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB��3��BC��4��P�ǶԽ���BD�ϵĶ��㣬��BPΪֱ����Բ����Բ�����ABCD�ı�����ʱ��BP�ij�Ϊ__��
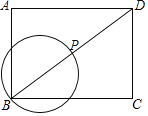
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��������ֽƬ![]() �У�
��![]() ��
��![]() cm��
cm��![]() cm����
cm����![]() �ֱ��ڱ�
�ֱ��ڱ�![]() �ϣ���
�ϣ���![]() �DZ�
�DZ�![]() ���е㣮�ֽ���ֽƬ��
���е㣮�ֽ���ֽƬ��![]() �۵���ʹ��
�۵���ʹ��![]() ���
���![]() �غϣ���
�غϣ���![]() ______cm��
______cm��
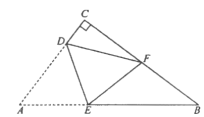
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���![]() �У���
�У���![]() �ֱ���
�ֱ���![]() �ϣ���
�ϣ���![]() ����
����![]() �ı�
�ı�![]() �ϵĸ�Ϊ
�ϵĸ�Ϊ![]() ��
��![]() �ı�
�ı�![]() �ϵĸ�Ϊ
�ϵĸ�Ϊ![]() ��
��
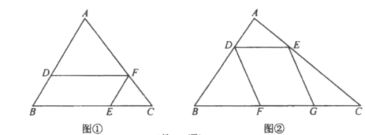
��1����![]() ��
��![]() ������ֱ�Ϊ3��1����
������ֱ�Ϊ3��1����![]() ��
��
��2����![]() ��
��![]() ���ı���
���ı���![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ����֤��
����֤��![]() ��
��
��3����ͼ�ڣ���![]() �У���
�У���![]() �ֱ���
�ֱ���![]() �ϣ���
�ϣ���![]() ��
��![]() �ϣ���
�ϣ���![]() ��
�� ![]() �� ��
�� ��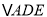 ��
��![]() ��
��![]() ������ֱ�Ϊ3�� 7�� 5����
������ֱ�Ϊ3�� 7�� 5����![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������������£�ij����ר������ij��Ʒ�Ƶ�������Ͳ���ɱ�Ϊ30Ԫ/����ÿ��������![]() �����������۵���
�����������۵���![]() ��Ԫ��֮�����һ�κ�����ϵ����ͼ��ʾ.
��Ԫ��֮�����һ�κ�����ϵ����ͼ��ʾ.
��1����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2������涨ÿ��������Ͳ��������������240���������۵���Ϊ����Ԫʱ��ÿ���ȡ�����������������Ƕ��٣�
��3��������������Ĺ�����ҵ��������ÿ������������о��150Ԫ��ϣ�����̣�Ϊ�˱�֤����ÿ��ʣ��������3600Ԫ����ȷ����������Ͳ���۵��۵ķ�Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BCΪֱ���ġ�O����CFB�ı�CF�ڵ�A��BMƽ�֡�ABC��AC�ڵ�M��AD��BC�ڵ�D��AD��BM�ڵ�N��ME��BC�ڵ�E��AB2=AF��AC��cos��ABD=![]() ��AD=12��
��AD=12��
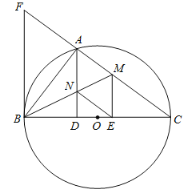
��1����֤����ABF�ס�ACB��
��2����֤��FB�ǡ�O�����ߣ�
��3��֤���ı���AMEN�����Σ���������ε����S��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com