
����Ŀ���������������̳��ﹺ���ܺ���90Ԫ����Ʒ�ס��ҡ��������Σ����мĵ�����20Ԫ���ҵĵ�����40Ԫ������Ʒ��һ�ι���������ǵڶ��ι�������������������Ʒ��һ�ι�������������Ʒ�ڶ��ι����������ȣ����ι�����Ʒ�ס��ҡ������������ܷ������±���
������Ʒ�� ����(��) | ������Ʒ�ҵ� ����(��) | ������Ʒ���� ����(��) | �����ܷ���(Ԫ) | |
��һ�ι��� | 4 | 440 | ||
�ڶ��ι��� | 7 | 490 |
(1)�����ι���ס��ҡ���������Ʒ���������ֱ��Ƕ��٣�
(2)���������̳�������������������������ǰ��������Ʒ�ס��ҡ�������������Ʒ�������ܺ�Ϊa�������й�������Ʒ�����Ǽ���Ʒ������3���������ܷ���Ϊ1 280Ԫ����a����Сֵ��
���𰸡���1�����ι���ס��ҡ���������Ʒ����������Ϊ15������2��38.
��������
��1����ڶ��ι�������Ʒx������������Ʒy�������һ�ι�������Ʒ2x��������Ʒy���������ܼ�=���ۡ�������ǰ���ι�����ܷ��ã����ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó�x��y��ֵ���ٷֱ����ι��ﹺ����������Ʒ������Ӽ��ɵó����ۣ�
��2��������ι�������Ʒm����������Ʒ3m��������Ʒ��a-4m�����������ܼ�=���ۡ�������Ϲ����ܷ���Ϊ1280Ԫ�����ɵĹ���a��m�Ķ�Ԫһ�η��̣����a��m��a-4m��Ϊ�Ǹ��������������a��m��ֵ��ȡ����Сֵ���ɵó����ۣ�
�⣺(1)��ڶ��ι�������Ʒx������������Ʒy�������һ�ι�������Ʒ2x��������Ʒy����
�����⣬�ã�![]()
��ã�![]()
��2x��y��4��15��x��7��y��15
�����ι���ס��ҡ���������Ʒ����������Ϊ15��.
(2)������ι�������Ʒm����������Ʒ3m��������Ʒ(a��4m)����
�����⣬�ã�20m��40��3m��(90��20��40)(a��4m)��1 280��
��a��![]()
��a��m��a��4m��Ϊ�Ǹ�������
��![]() ��
��![]() ��
��![]()
��a����СֵΪ38.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������C�ڡ�O�ϣ��Ҳ���A��B�����غϣ�����C�����߽�AB���ӳ����ڵ�D������AC��BC������ABC��53�������D�Ķ����ǣ�������

A. 16��B. 18��C. 26.5��D. 37.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������y��ax2+bx+c�ĶԳ���Ϊֱ��x��1���ҹ��㣨3��0�������н��ۣ���abc��0����a��b+c��0����2a+b��0����b2��4ac��0����ȷ���У�����������
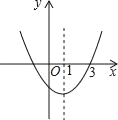
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ķ��쾭����ѩ��Ϊ�������ѩ��Ч�ʣ���������������ѩ������֪һ̨��ѩ���Ĺ���Ч���൱��һ���������˵�200����������̨��ѩ������9000�����Ļ�ѩ��Ҫ��150����������������Щ��ѩ����2Сʱ����һ̨��ѩ��ÿСʱ��ѩ���������ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y1��kx+b��y2��x+a��ͼ����ͼ��ʾ�������н��ۣ���k��0����a��0������x��3ʱ��y1��y2������y1��0��y2��0ʱ����a��x��4��������ȷ�ĸ����ǣ�������

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��������ϣ���������������⣺��ͼ1����ֱ�������εĸ���Ϊֱ���ֱ���������Բ����ֱ�������ε�����ɱ�ʾ�����������ε����֮�ͣ��ֽ�������ԲֽƬ��ֱ�������εĸ������·��۵õ�ͼ2���ѽ�С�����Ű�ԲֽƬ���ص����������ΪS1�����ԲֽƬδ�����Dz��ֵ������ΪS2����ֱ�������ε�����ɱ�ʾ�ɣ�������
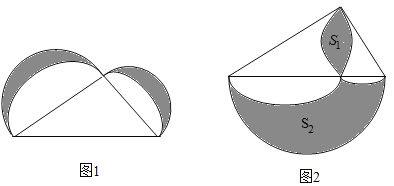
A.S1+S2B.S2��S1C.S2��2S1D.S1S2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�������²�Ʒ1520kg��ΪѰ����ʵ����ۼ۸�����8��������������470kg��ͳ�Ʒ���ÿ���������y��ǧ�ˣ������ۼ۸�x��Ԫ/ǧ�ˣ�֮�����㺯����ϵy����x+120��
��1��������8���˾���������ֲ�Ʒ�����ۼ۸�Ϊ50Ԫ/ǧ�ˣ�����ÿ�춼������۸����ۣ������µIJ�Ʒ���ö�����ȫ�����ꣿ
��2���ڣ�1���������£���˾��������9�����ʣ��IJ�Ʒ������5����ȫ�����꣬��ʱ��Ҫ����ȷ��һ�����ۼ۸�ʹ���涼���µļ۸����ۣ���ô��ȷ���ļ۸���߲�����ÿǧ�˶���Ԫ���������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=-![]() x+2��x�ύ�ڵ�B����y�ύ�ڵ�C����֪���κ�����ͼ����B��C�͵�A(-1��0)��
x+2��x�ύ�ڵ�B����y�ύ�ڵ�C����֪���κ�����ͼ����B��C�͵�A(-1��0)��
(1)��B��C��������꣮
(2)��ö��κ����Ľ���ʽ��
(3)�������ߵĶԳ�����x��Ľ���Ϊ��D�����������ߵĶԳ������Ƿ���ڵ�P��ʹ��PCD����CDΪ���ĵ���������?������ڣ�ֱ��д����P�����ꣻ��������ڣ���˵�����ɣ�
(4)��E���߶�BC�ϵ�һ�����㣬����E��x��Ĵ������������ཻ�ڵ�F������E�˶���ʲôλ��ʱ���ı���CDBF��������?����ı���CDBF������������ʱ��E�����꣮
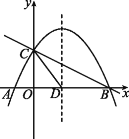
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����������Ϊ
����������Ϊ![]() ����
����![]() ��Ľ�����
��Ľ�����![]() ��
��![]() ֮��(�����˵�)�����½��ۣ� ��
֮��(�����˵�)�����½��ۣ� ��![]() ����
����![]() ����
����![]() ���ܹ���
���ܹ���![]() �ķ���
�ķ���![]() û��ʵ������������ȷ�Ľ����У� ��
û��ʵ������������ȷ�Ľ����У� ��
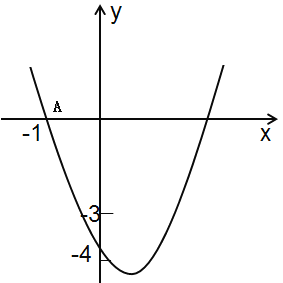
A.4��B.3��C.2��D.1��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com