
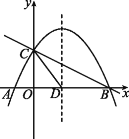
ЁОЬтФПЁПШчЭМЃЌжБЯпy=-![]() x+2гыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуCЃЌвбжЊЖўДЮКЏЪ§ЕФЭМЯѓОЙ§ЕуBЃЌCКЭЕуA(-1ЃЌ0)ЃЎ
x+2гыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуCЃЌвбжЊЖўДЮКЏЪ§ЕФЭМЯѓОЙ§ЕуBЃЌCКЭЕуA(-1ЃЌ0)ЃЎ
(1)ЧѓBЃЌCСНЕуЕФзјБъЃЎ
(2)ЧѓИУЖўДЮКЏЪ§ЕФНтЮіЪНЃЎ
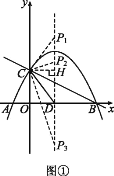
(3)ШєХзЮяЯпЕФЖдГЦжсгыxжсЕФНЛЕуЮЊЕуDЃЌдђдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкЕуPЃЌЪЙЁїPCDЪЧвдCDЮЊбќЕФЕШбќШ§НЧаЮ?ШчЙћДцдкЃЌжБНгаДГіЕуPЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
(4)ЕуEЪЧЯпЖЮBCЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуEзїxжсЕФДЙЯпгыХзЮяЯпЯрНЛгкЕуFЃЌЕБЕуEдЫЖЏЕНЪВУДЮЛжУЪБЃЌЫФБпаЮCDBFЕФУцЛ§зюДѓ?ЧѓГіЫФБпаЮCDBFЕФзюДѓУцЛ§МАДЫЪБЕуEЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉB(4ЃЌ0)ЃЌC(0ЃЌ2)ЃЛЃЈ2ЃЉy=-![]() x2+
x2+![]() x+2ЃЛЃЈ3ЃЉДцдкЃЌP1(
x+2ЃЛЃЈ3ЃЉДцдкЃЌP1(![]() ЃЌ4)ЃЌP2(
ЃЌ4)ЃЌP2(![]() )ЃЌP3(
)ЃЌP3(![]() ЃЌ-
ЃЌ-![]() )ЃЛЃЈ4ЃЉЕБa=2ЪБЃЌSЫФБпаЮCDBFЕФзюДѓжЕ=
)ЃЛЃЈ4ЃЉЕБa=2ЪБЃЌSЫФБпаЮCDBFЕФзюДѓжЕ=![]() ЃЌДЫЪБE(2ЃЌ1)ЃЎ
ЃЌДЫЪБE(2ЃЌ1)ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЗжБ№СюНтЮіЪНy=-![]() x+2жаx=0ЃЌy=0ЃЌЧѓГіЕуBЃЌЕуCЕФзјБъЃЛ
x+2жаx=0ЃЌy=0ЃЌЧѓГіЕуBЃЌЕуCЕФзјБъЃЛ
ЃЈ2ЃЉЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ![]() ЃЌНЋЕуAЁЂBЁЂCЕФзјБъДњШыНтЮіЪНЃЌЧѓГіaЃЌbЃЌcЕФжЕЃЌНјЖјЧѓГіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЌНЋЕуAЁЂBЁЂCЕФзјБъДњШыНтЮіЪНЃЌЧѓГіaЃЌbЃЌcЕФжЕЃЌНјЖјЧѓГіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉЕФНтЮіЪНЧѓГіЖЅЕузјБъЃЌдйгЩЙДЙЩЖЈРэЧѓГіCDЕФжЕЃЌдйвдЕуCЮЊдВаФЃЌCDЮЊАыОЖзїЛЁНЛЖдГЦжсгк![]() ЃЌвдЕуDЮЊдВаФЃЌCDЮЊАыОЖзїдВНЛЖдГЦжсгк
ЃЌвдЕуDЮЊдВаФЃЌCDЮЊАыОЖзїдВНЛЖдГЦжсгк![]() ЃЌ
ЃЌ![]() ЃЌзїCEДЙжБЖдГЦжсгкЕуEЃЌгЩЕШбќШ§НЧаЮЕФаджЪКЭЙДЙЩЖЈРэОЭПЩвдЧѓГіНсТлЃЛ
ЃЌзїCEДЙжБЖдГЦжсгкЕуEЃЌгЩЕШбќШ§НЧаЮЕФаджЪКЭЙДЙЩЖЈРэОЭПЩвдЧѓГіНсТлЃЛ
ЃЈ4ЃЉЩшЕуEЕФзјБъЮЊ![]() ЃЌОЭПЩвдБэЪОГіFЕФзјБъЃЌгЩ
ЃЌОЭПЩвдБэЪОГіFЕФзјБъЃЌгЩ![]() ЧѓГіSгыaЕФЙиЯЕЪНЃЌгЩЖўДЮКЏЪ§ЕФаджЪОЭПЩвдЧѓГіНсТлЃЎ
ЧѓГіSгыaЕФЙиЯЕЪНЃЌгЩЖўДЮКЏЪ§ЕФаджЪОЭПЩвдЧѓГіНсТлЃЎ
НтЃК(1)дкy=-![]() x+2жаЃЌСюx=0ЃЌПЩЕУy=2ЃЌСюy=0ЃЌПЩЕУx=4ЃЌ
x+2жаЃЌСюx=0ЃЌПЩЕУy=2ЃЌСюy=0ЃЌПЩЕУx=4ЃЌ
МДB(4ЃЌ0)ЃЌC(0ЃЌ2)ЃЎ
(2)ЩшЖўДЮКЏЪ§ЕФНтЮіЪНЮЊy=ax2+bx+cЃЌ
НЋЕуAЃЌBЃЌCЕФзјБъДњШыНтЮіЪНЃЌЕУ
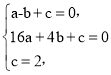 ЃЌ
ЃЌ
НтЕУ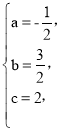
МДИУЖўДЮКЏЪ§ЕФНтЮіЪНЮЊy=-![]() x2+
x2+![]() x+2ЃЎ
x+2ЃЎ
(3)ДцдкЃЎЁпy=-![]() x2+
x2+![]() x+2ЃЌ
x+2ЃЌ
Ёрy=-![]() (x-
(x-![]() )2+
)2+![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФЖдГЦжсЪЧжБЯпx=![]() ЃЌЁрOD=
ЃЌЁрOD=![]() ЃЎ
ЃЎ
ЁпC(0ЃЌ2)ЃЌЁрOC=2ЃЎ
дкRtЁїOCDжаЃЌгЩЙДЙЩЖЈРэЃЌЕУCD=![]() ЃЎ
ЃЎ
ЁпЁїPCDЪЧвдCDЮЊбќЕФЕШбќШ§НЧаЮЃЌ
ЁрCP1=DP2=DP3=CDЃЎ
ШчЭМЂйЫљЪОЃЌзїCHЁЭЖдГЦжсгкЕуHЃЌЁрHP1=HD=2ЃЌ
ЁрDP1=4ЃЎ
ЁрP1(![]() ЃЌ4)ЃЌP2(
ЃЌ4)ЃЌP2(![]() )ЃЌP3(
)ЃЌP3(![]() ЃЌ-
ЃЌ-![]() )ЃЎ
)ЃЎ
(4)ЁпB(4ЃЌ0)ЃЌC(0ЃЌ2)ЃЌ
ЁржБЯпBCЕФНтЮіЪНЮЊy=-![]() x+2ЃЎ
x+2ЃЎ
ШчЭМЂкЃЌЙ§ЕуCзїCMЁЭEFгкЕуMЃЌ
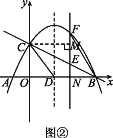
ЩшE(aЃЌ-![]() a+2)ЃЌF(aЃЌ-
a+2)ЃЌF(aЃЌ-![]() a2+
a2+![]() a+2)ЃЌ
a+2)ЃЌ
ЁрEF=-![]() a2+
a2+![]() a+2-(-
a+2-(-![]() a+2)=-
a+2)=-![]() a2+2a(0ЁмaЁм4)ЃЎ
a2+2a(0ЁмaЁм4)ЃЎ
ЁпSЫФБпаЮCDBF=SЁїBCD+SЁїCEF+SЁїBEF=![]() BDЁЄOC+
BDЁЄOC+![]() EFЁЄCM+
EFЁЄCM+![]() EFЁЄBN
EFЁЄBN
=![]() ЁС(4-
ЁС(4-![]() )ЁС2+
)ЁС2+![]() a(-
a(-![]() a2+2a)+
a2+2a)+![]() (4-a)( -
(4-a)( -![]() a2+2a)
a2+2a)
=-a2+4a+![]()
=-(a-2)2+![]() ЃЌ
ЃЌ
ЁрЕБa=2ЪБЃЌSЫФБпаЮCDBFЕФзюДѓжЕ=![]() ЃЌДЫЪБE(2ЃЌ1)ЃЎ
ЃЌДЫЪБE(2ЃЌ1)ЃЎ


 ШЋгХГхДЬ100ЗжЯЕСаД№АИ
ШЋгХГхДЬ100ЗжЯЕСаД№АИ гЂВХЕуНђЯЕСаД№АИ
гЂВХЕуНђЯЕСаД№АИ КьЙћзгШ§МЖВтЪдОэЯЕСаД№АИ
КьЙћзгШ§МЖВтЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдРЌЛјНјааЗжРрЭЖЗХЃЌФмЬсИпРЌЛјДІРэКЭдйРћгУЕФаЇТЪЃЌМѕЩйЮлШОЃЌБЃЛЄЛЗОГЃЎЮЊСЫМьВщРЌЛјЗжРрЕФТфЪЕЧщПіЃЌФГОгЮЏЛсГЩСЂСЫМзЁЂввСНИіМьВщзщЃЌВЩШЁЫцЛњГщВщЕФЗНЪНЗжБ№ЖдЯНЧјФкЕФAЃЌBЃЌCЃЌDЫФИіаЁЧјНјааМьВщЃЌВЂЧвУПИіаЁЧјВЛжиИДМьВщЃЎ
ЃЈ1ЃЉМззщГщЕНAаЁЧјЕФИХТЪЪЧЖрЩйЃЛ
ЃЈ2ЃЉЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓМззщГщЕНAаЁЧјЃЌЭЌЪБввзщГщЕНCаЁЧјЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭѕТшТшдкСЋЛЈЩЬГЁРяЙКТђЕЅМлзмКЭЪЧ90дЊЕФЩЬЦЗМзЁЂввЁЂБћЙВСНДЮЃЌЦфжаМзЕФЕЅМлЪЧ20дЊЃЌввЕФЕЅМлЪЧ40дЊЃЌМзЩЬЦЗЕквЛДЮЙКТђЕФЪ§СПЪЧЕкЖўДЮЙКТђЪ§СПЕФСНБЖЃЌввЩЬЦЗЕквЛДЮЙКТђЕФЪ§СПгыБћЩЬЦЗЕкЖўДЮЙКТђЕФЪ§СПЯрЕШЃЌСНДЮЙКТђЩЬЦЗМзЁЂввЁЂБћЕФЪ§СПКЭзмЗбгУШчЯТБэЃК
ЙКТђЩЬЦЗМзЕФ Ъ§СП(Иі) | ЙКТђЩЬЦЗввЕФ Ъ§СП(Иі) | ЙКТђЩЬЦЗБћЕФ Ъ§СП(Иі) | ЙКТђзмЗбгУ(дЊ) | |
ЕквЛДЮЙКЮя | 4 | 440 | ||
ЕкЖўДЮЙКЮя | 7 | 490 |
(1)ЧѓСНДЮЙКТђМзЁЂввЁЂБћШ§жжЩЬЦЗЕФзмЪ§СПЗжБ№ЪЧЖрЩйЃП
(2)гЩгкСЋЛЈЩЬГЁЮяУРМлСЎЃЌЭѕТшТшДђЫуЕкШ§ДЮЧАЭљЙКТђЩЬЦЗМзЁЂввЁЂБћЃЌЩшШ§жжЩЬЦЗЕФЪ§СПзмКЭЮЊaИіЃЌЦфжаЙКТђввЩЬЦЗЪ§СПЪЧМзЩЬЦЗЪ§СПЕФ3БЖЃЌЙКТђзмЗбгУЮЊ1 280дЊЃЌЧѓaЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
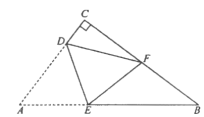
ЁОЬтФПЁПШчЭМЃЌжБНЧШ§НЧаЮжНЦЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() cmЃЌ
cmЃЌ![]() cmЃЌЕу
cmЃЌЕу![]() ЗжБ№дкБп
ЗжБ№дкБп![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() ЪЧБп
ЪЧБп![]() ЕФжаЕуЃЎЯжНЋИУжНЦЌби
ЕФжаЕуЃЎЯжНЋИУжНЦЌби![]() елЕўЃЌЪЙЕу
елЕўЃЌЪЙЕу![]() гыЕу
гыЕу![]() жиКЯЃЌдђ
жиКЯЃЌдђ![]() ______cmЃЎ
______cmЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЃЌдк![]() жаЃЌЕу
жаЃЌЕу![]() ЗжБ№дк
ЗжБ№дк![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЎЩш
ЃЎЩш![]() ЕФБп
ЕФБп![]() ЩЯЕФИпЮЊ
ЩЯЕФИпЮЊ![]() ЃЌ
ЃЌ![]() ЕФБп
ЕФБп![]() ЩЯЕФИпЮЊ
ЩЯЕФИпЮЊ![]() ЃЎ
ЃЎ
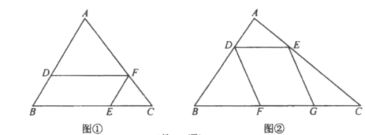
ЃЈ1ЃЉШє![]() ЁЂ
ЁЂ![]() ЕФУцЛ§ЗжБ№ЮЊ3ЃЌ1ЃЌдђ
ЕФУцЛ§ЗжБ№ЮЊ3ЃЌ1ЃЌдђ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩш![]() ЁЂ
ЁЂ![]() ЁЂЫФБпаЮ
ЁЂЫФБпаЮ![]() ЕФУцЛ§ЗжБ№ЮЊ
ЕФУцЛ§ЗжБ№ЮЊ![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМЂкЃЌдк![]() жаЃЌЕу
жаЃЌЕу![]() ЗжБ№дк
ЗжБ№дк![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() дк
дк![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌ
ЃЌ ![]() ЃЎ Шє
ЃЎ Шє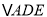 ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФУцЛ§ЗжБ№ЮЊ3ЃЌ 7ЃЌ 5ЃЌЧѓ
ЕФУцЛ§ЗжБ№ЮЊ3ЃЌ 7ЃЌ 5ЃЌЧѓ![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
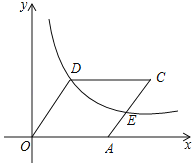
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌКЏЪ§y=![]() ЃЈkЃО0ЃЌxЃО0ЃЉЕФЭМЯѓОЙ§СтаЮOACDЕФЖЅЕуDКЭБпACЕФжаЕуEЃЌШєСтаЮOACDЕФБпГЄЮЊ3ЃЌдђkЕФжЕЮЊ_____ЃЎ
ЃЈkЃО0ЃЌxЃО0ЃЉЕФЭМЯѓОЙ§СтаЮOACDЕФЖЅЕуDКЭБпACЕФжаЕуEЃЌШєСтаЮOACDЕФБпГЄЮЊ3ЃЌдђkЕФжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
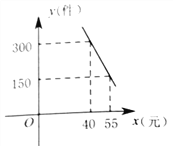
ЁОЬтФПЁПЁАбяжнЦсЦїЁБУћбяЬьЯТЃЌФГЭјЕъзЈУХЯњЪлФГжжЦЗХЦЕФЦсЦїБЪЭВЃЌГЩБОЮЊ30дЊ/МўЃЌУПЬьЯњЪлСП![]() ЃЈМўЃЉгыЯњЪлЕЅМл
ЃЈМўЃЉгыЯњЪлЕЅМл![]() ЃЈдЊЃЉжЎМфДцдквЛДЮКЏЪ§ЙиЯЕЃЌШчЭМЫљЪО.
ЃЈдЊЃЉжЎМфДцдквЛДЮКЏЪ§ЙиЯЕЃЌШчЭМЫљЪО.
ЃЈ1ЃЉЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШчЙћЙцЖЈУПЬьЦсЦїБЪЭВЕФЯњЪлСПВЛЕЭгк240МўЃЌЕБЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌУПЬьЛёШЁЕФРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйЃП
ЃЈ3ЃЉИУЭјЕъЕъжїШШаФЙЋвцЪТвЕЃЌОіЖЈДгУПЬьЕФЯњЪлРћШѓжаОшГі150дЊИјЯЃЭћЙЄГЬЃЌЮЊСЫБЃжЄОшПюКѓУПЬьЪЃгрРћШѓВЛЕЭгк3600дЊЃЌЪдШЗЖЈИУЦсЦїБЪЭВЯњЪлЕЅМлЕФЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁб![]() ОЙ§
ОЙ§![]() СНЕуЃЌ
СНЕуЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧЛЁABЕФжаЕуЃЌСЌНг
ЪЧЛЁABЕФжаЕуЃЌСЌНг![]() НЛЯв
НЛЯв![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЁб![]() ЕФАыОЖЃЛ
ЕФАыОЖЃЛ
ЃЈ2ЃЉЙ§Еу![]() ЗжБ№зї
ЗжБ№зї![]() ЕФЦНааЯпЃЌНЛгкЕу
ЕФЦНааЯпЃЌНЛгкЕу![]() ЪЧЁб
ЪЧЁб![]() ЩЯвЛЕуЃЌСЌНг
ЩЯвЛЕуЃЌСЌНг![]() НЛЁб
НЛЁб![]() гкЕу
гкЕу![]() ЃЌЧв
ЃЌЧв![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕЅЮЛГЄЖШЮЊ1УзЕФЦНУцжБНЧзјБъЯЕжаЃЌЧњЯпЪЧгЩАыОЖЮЊ2УзЃЌдВаФНЧЮЊ![]() ЕФ
ЕФ![]() ЖрДЮИДжЦВЂЪзЮВСЌНгЖјГЩЃЎЯжгавЛЕуPДгA(AЮЊзјБъдЕу)ГіЗЂЃЌвдУПУы
ЖрДЮИДжЦВЂЪзЮВСЌНгЖјГЩЃЎЯжгавЛЕуPДгA(AЮЊзјБъдЕу)ГіЗЂЃЌвдУПУы![]() УзЕФЫйЖШбиЧњЯпЯђгвдЫЖЏЃЌдђдкЕк2019УыЪБЕуPЕФзнзјБъЮЊ( )
УзЕФЫйЖШбиЧњЯпЯђгвдЫЖЏЃЌдђдкЕк2019УыЪБЕуPЕФзнзјБъЮЊ( )
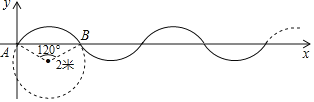
A. Љ2B. Љ1C. 0D. 1
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com