
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() 是内心,
是内心,![]() 是外心,则
是外心,则![]() 等于( )
等于( )

A.130°B.135°C.140°D.145°
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系中,一次函数的图象l![]() 与y轴交于点A(0 , 2),与一次函数y=x﹣3的图象l
与y轴交于点A(0 , 2),与一次函数y=x﹣3的图象l![]() 交于点E(m ,﹣5).
交于点E(m ,﹣5).
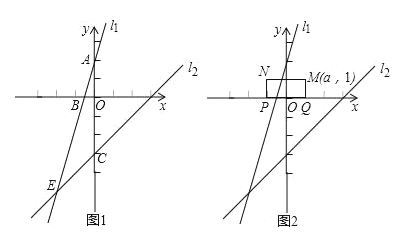
(1)m=__________;
(2)直线l![]() 与x轴交于点B,直线l
与x轴交于点B,直线l![]() 与y轴交于点C,求四边形OBEC的面积;
与y轴交于点C,求四边形OBEC的面积;
(3)如图2,已知矩形MNPQ,PQ=2,NP=1,M(a,1),矩形MNPQ的边PQ在x轴上平移,若矩形MNPQ与直线l![]() 或l
或l![]() 有交点,直接写出a的取值范围_____________________________
有交点,直接写出a的取值范围_____________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于合肥滨湖新区的渡江战役纪念馆,实物图如图1所示,示意图如图2所示.某学校数学兴趣小组通过测量得知,纪念馆外轮廓斜坡AB的坡度i=1:![]() ,底基BC=50m,∠ACB=135°,求馆顶A离地面BC的距离.(结果精确到0.1m,参考数据:
,底基BC=50m,∠ACB=135°,求馆顶A离地面BC的距离.(结果精确到0.1m,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,且不与A、B两点重合,过点C的切线交AB的延长线于点D,连接AC,BC,若∠ABC=53°,则∠D的度数是( )

A. 16°B. 18°C. 26.5°D. 37.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古贤常说万物皆自然,而古希腊学者说万物皆数.同学们还记得我们最初接触的数就是“自然数”吧!在数的学习过程中,我们会对其中一些具有某种特性的自然数进行研究,我们研究了奇数、偶数、质数、合数等.现在我们来研究另一种特珠的自然数—“![]() 喜数”.
喜数”.
定义:对于一个两位自然数,如果它的个位和十位上的数字均不为零,且它正好等于其个位和十位上的数字的和的![]() 倍(
倍(![]() 为正整数),我们就说这个自然数是一个“
为正整数),我们就说这个自然数是一个“![]() 喜数”.
喜数”.
例如:24就是一个“4喜数”,因为![]()
25就不是一个“![]() 喜数”因为
喜数”因为![]()
(1)判断44和72是否是“![]() 喜数”?请说明理由;
喜数”?请说明理由;
(2)试讨论是否存在“7喜数”若存在请写出来,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() .
.
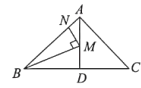
(1)如图所示,点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上,且
上,且![]() ,当
,当![]() ,
,![]() 时,求线段
时,求线段![]() 的长;
的长;
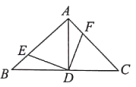
(2)如图所示,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,求证:
,求证:![]() ;
;
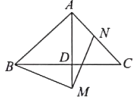
(3)如图所示,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 上,且
上,且![]() ,请直接写出
,请直接写出![]() ,
,![]() ,
,![]() 三者的等量关系式.
三者的等量关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
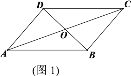
【题目】我们把有两边对应相等,且夹角互补(不相等)的两个三角形叫做“互补三角形”,如图1,□ABCD中,△AOB和△BOC是“互补三角形”.
(1)写出图1中另外一组“互补三角形”_______;
(2)在图2中,用尺规作出一个△EFH,使得△EFH和△EFG为“互补三角形”,且△EFH和△EFG在EF同侧,并证明这一组“互补三角形”的面积相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线y=ax2+bx+c的对称轴为直线x=1,且过点(3,0),下列结论:①abc>0;②a﹣b+c<0;③2a+b>0;④b2﹣4ac>0;正确的有( )个.
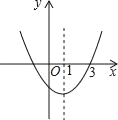
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研制了新产品1520kg,为寻求合适的销售价格,进行了8天试销,共销售470kg.统计发现每天的销售量y(千克)与销售价格x(元/千克)之间满足函数关系y=﹣x+120.
(1)在试销8天后,公司决定将这种产品的销售价格定为50元/千克,并且每天都按这个价格销售,则余下的产品再用多少天全部售完?
(2)在(1)的条件下,公司继续销售9天后,发现剩余的产品必须在5天内全部售完,此时需要重新确定一个销售价格,使后面都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com