
【题目】如图,AB为⊙O的直径,点C为![]() 下方的一动点,连结OC,过点O作OD⊥OC交BC于点D,过点C作AB的垂线,垂足为F,交DO的延长线于点E.
下方的一动点,连结OC,过点O作OD⊥OC交BC于点D,过点C作AB的垂线,垂足为F,交DO的延长线于点E.
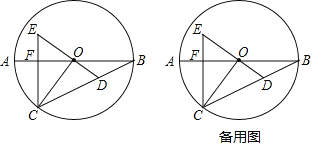
(1)求证:EC=ED.
(2)当OE=OD,AB=4时,求OE的长.
(3)设![]() =x,tanB=y.
=x,tanB=y.
①求y关于x的函数表达式;
②若△COD的面积是△BOD的面积的3倍,求y的值.
【答案】(1)见解析;(2)OE=![]() ;(3)①y=
;(3)①y=![]() (0<x<1),②y=
(0<x<1),②y=![]() .
.
【解析】
(1)先证明∠ECD=∠EDC,即可证明EC=ED;
(2)先证明△ECD是等边三角形,即可说明∠E=60°,然后再说明△EOC是直角三角形,最后解直角三角形即可;
(3)①连接AC.先证明x=![]() =
=![]() ,再证得
,再证得![]() ;令OC=k,则OF=kx,然后再利用勾股定理求得CF、AF,即可求得函数解析式;
;令OC=k,则OF=kx,然后再利用勾股定理求得CF、AF,即可求得函数解析式;
②作OH⊥BC于H,设BD=m,根据相似三角形的性质用m表示出OH、BH,然后代入函数解析式即可.
(1)证明:∵OD⊥OC,
∴∠COD=90°,
∴∠OCD+∠ODC=90°,
∵EC⊥AB,
∴∠CEB=90°,
∴∠B+∠ECB=90°,
∵OC=OB,
∴∠B=∠OCD,
∴∠ODC=∠ECB,
∴EC=EB.
(2)解:∵OE=OD,OC⊥ED,
∴CE=CE,
∵EC=ED,
∴EC=ED=CD,
∴△ECD是等边三角形,
∵∠E=60°,
在Rt△EOC中,
∵∠EOC=90°,OC=![]() AB=2,
AB=2,
∴OE=![]() =
=![]() .
.
(3)解:①连接AC.
∵EC=ED,∠EOC=90°
∴![]() =
=![]() =sin∠ECO,
=sin∠ECO,
∵∠OFC=90°,
∴sin∠ECO=![]() ,
,
∴x=![]() =
=![]() ,
,
∵AB是直径,
∴∠ACB=90°,
∵CE⊥AB,
∴∠AFC=90°,
∴∠ACF+∠A=90°,∠B+∠A=90°,
∴∠ACF=∠B,
∴tan∠B=tan∠ACF=![]() =y,
=y,
令OC=k,则OF=kx,CF=![]() =
=![]() =k
=k![]() ,
,
∴AF=OA﹣OF=k﹣kx=k(1﹣x),
∴y=![]() =
=![]() =
=![]() (0<x<1).
(0<x<1).
②作OH⊥BC于H.设BD=m,
∵△COD的面积是△BOD的面积的3倍,
∴CD=3BD=3m,CB=4m,
∵OH⊥BC,
∴CH=BH=2m,
∴HD=m,
∵∠OCH+∠COH=90°,∠COH+∠DOH=90°,
∴∠OCH=∠DOH,
∵∠OHC=∠OHD=90°,
∴△OHC∽△DHO,
∴![]() =
=![]() ,
,
∴OH2=2m2,
∴OH=![]() m,
m,
∴y=tanB=![]() =
=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
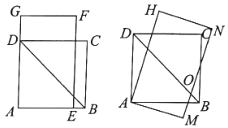
【题目】如图所示,四边形![]() 是边长为
是边长为![]() 的正方形,长方形
的正方形,长方形![]() 的宽
的宽![]() ,长
,长![]() .将长方形
.将长方形![]() 绕点
绕点![]() 顺时针旋转15°得到长方形
顺时针旋转15°得到长方形![]() (如图所示),这时
(如图所示),这时![]() 与
与![]() 相交于点
相交于点![]() .则在图中,
.则在图中,![]() ,
,![]() 两点间的距离是( )
两点间的距离是( )
A.![]() B.5C.
B.5C.![]() D.7
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读以下材料,并完成相应任务:
斐波那契(约1170-1250)是意大利数学家.1202年,撰写了《算盘书》一书,他是第一个研究了印度和阿拉伯数学理论的欧洲人,他还曾在埃及、叙利亚、希腊,以及意大利西西里和法国普罗旺斯等地研究数学.他研究了一列非常奇妙的数:0,1,1,2,3,5,8,13,21,34,55,89,144……这列数,被称为斐波那契数列.其特点是从第3项开始,每一项都等于前两项之和,斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.

任务:(1)填写下表并写出通过填表你发现的规律:
项 | 第2项 | 第3项 | 第4项 | 第5项 | 第6项 | 第7项 | 第8项 | 第9项 | … |
这一项的平方 | 1 | 1 | 4 | 9 | 25 | ________ | _______ | 441 | … |
这一项的前、后两项的积 | 0 | 2 | 3 | 10 | 24 | _______ | _______ | 442 | … |
规律:_____________;
(2)现有长为![]() 的铁丝,要截成
的铁丝,要截成![]() 小段,每段的长度不小于
小段,每段的长度不小于![]() ,如果其中任意三小段都不能拼成三角形,则
,如果其中任意三小段都不能拼成三角形,则![]() 的最大值为___________________.
的最大值为___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,且AB=6.点C是⊙O上的一动点,连接AC,BC,在AC的延长线上取一点D,使得∠CBD=∠DAB,点G为DB的中点,点E为BG的中点,连接AE交BC于点F.
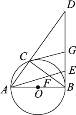
(1)试判断直线BD与⊙O的位置关系,并说明理由;
(2)当∠CGB=60°时,求![]() 的长;
的长;
(3)当AE∥CG时,连接GF,若AF=4,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了解全校2000名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选,将调查得到的结果绘制成如图所示的统计图和频数表(均不完整).
到校方式 | 频数 | 频率 |
自行车 | 24 | 0.3 |
步行 | ||
公交车 | 0.325 | |
私家车 | 10 | |
其他 | 4 |
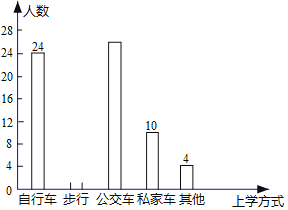
由图表中给出的信息回答下列问题:
(1)问:在这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图.
(3)估计全校所有学生中有多少人步行上学.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有2个白球、1个红球、1个黄球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好是白球的概率是 ;
(2)从中任意摸出2个球,求2个球都是白球的概率(用画树状图或列表等方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题:①若![]() =-a,则a≤0;②若a>
=-a,则a≤0;②若a>![]() ,则a2>b2;③两个位似图形一定是相似图形;④平行四边形的两组对边分别相等.其中原命题与逆命题均为真命题的个数是( )
,则a2>b2;③两个位似图形一定是相似图形;④平行四边形的两组对边分别相等.其中原命题与逆命题均为真命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四种说法:
①如果一个角的两边与另一个角的两边分别平行,那么这两个角相等;
②将2020减去它的![]() ,再减去余下的
,再减去余下的![]() ,再减去余下的
,再减去余下的![]() ,再减去余下的
,再减去余下的![]() ,……,依此类推,直到最后减去余下的
,……,依此类推,直到最后减去余下的![]() ,最后的结果是1;
,最后的结果是1;
③实验的次数越多,频率越靠近理论概率;
④对于任何实数x、y,多项式![]() 的值不小于2.其中正确的个数是()
的值不小于2.其中正确的个数是()
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com