
【题目】请阅读以下材料,并完成相应任务:
斐波那契(约1170-1250)是意大利数学家.1202年,撰写了《算盘书》一书,他是第一个研究了印度和阿拉伯数学理论的欧洲人,他还曾在埃及、叙利亚、希腊,以及意大利西西里和法国普罗旺斯等地研究数学.他研究了一列非常奇妙的数:0,1,1,2,3,5,8,13,21,34,55,89,144……这列数,被称为斐波那契数列.其特点是从第3项开始,每一项都等于前两项之和,斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.

任务:(1)填写下表并写出通过填表你发现的规律:
项 | 第2项 | 第3项 | 第4项 | 第5项 | 第6项 | 第7项 | 第8项 | 第9项 | … |
这一项的平方 | 1 | 1 | 4 | 9 | 25 | ________ | _______ | 441 | … |
这一项的前、后两项的积 | 0 | 2 | 3 | 10 | 24 | _______ | _______ | 442 | … |
规律:_____________;
(2)现有长为![]() 的铁丝,要截成
的铁丝,要截成![]() 小段,每段的长度不小于
小段,每段的长度不小于![]() ,如果其中任意三小段都不能拼成三角形,则
,如果其中任意三小段都不能拼成三角形,则![]() 的最大值为___________________.
的最大值为___________________.
【答案】(1)64,169,65,168;规律:从第二项起,偶数项的平方比这一项的前、后两项的积大1,奇数项的平方比这一项的前、后两项的积小1;(2)5
【解析】
(1)根据表格中已有的数据可得到如下规律:从第二项起,偶数项的平方比这一项的前、后两项的积大1,奇数项的平方比这一项的前、后两项的积小1,进而填表即可;
(2)根据三角形的三边关系;三角形两边之和大于第三边,由于每段的长为不小于1的整数,所以设最小的是1,又由于其中任意三段都不能拼成三角形,所以每段长是:1,1,2,3,5,然后依此类推,最后每段的总和要不大于15即可.
解:(1)填表如下:
项 | 第2项 | 第3项 | 第4项 | 第5项 | 第6项 | 第7项 | 第8项 | 第9项 | … |
这一项的平方 | 1 | 1 | 4 | 9 | 25 | 64 | 169 | 441 | … |
这一项的前、后两项的积 | 0 | 2 | 3 | 10 | 24 | 65 | 168 | 442 | … |
规律:从第二项起,偶数项的平方比这一项的前、后两项的积大1,奇数项的平方比这一项的前、后两项的积小1.
(2)构成三角形的条件是任何两边之和大于第三边,因此构不成三角形的条件就是存在两边之和不超过第三边,要使截得的小铁丝数量最多,那么截成的小段铁丝应尽可能的短.已知截成的铁丝最小为![]() ,因此可以先截取2个
,因此可以先截取2个![]() ,第三段铁丝就是
,第三段铁丝就是![]() ,即从第三段开始,其长度是前两段铁丝长度的和.若第四段铁丝为
,即从第三段开始,其长度是前两段铁丝长度的和.若第四段铁丝为![]() ,第五段铁丝为
,第五段铁丝为![]() ,这时剩下
,这时剩下![]() ,由于
,由于![]() ,因此最后一段为
,因此最后一段为![]() .则截成的铁丝的长度依次为:
.则截成的铁丝的长度依次为:![]() ,所以最多能截成5段.
,所以最多能截成5段.


科目:初中数学 来源: 题型:
【题目】某校九年级数学模拟测试中,六名学生的数学成绩如下表所示,下列关于这组数据描述正确的是( )
姓名 | 小红 | 小明 | 小东 | 小亮 | 小丽 | 小华 |
成绩(分) | 110 | 106 | 109 | 111 | 108 | 110 |
A.众数是110B.方差是16
C.平均数是109.5D.中位数是109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对博鳌论坛会的了解情况,某中学随机抽取了部分学生进行问卷调查,将调查结果记作“![]() 非常了解,
非常了解,![]() 了解,
了解,![]() 了解较少,
了解较少,![]() 不了解.”四类分别统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
不了解.”四类分别统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
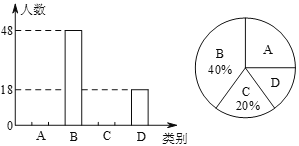
(1)此次共调查了______名学生;扇形统计图中![]() 所在的扇形的圆心角度数为______;
所在的扇形的圆心角度数为______;
(2)将条形统计图补充完整;
(3)若该校共有1600名学生,请你估计对博鳌论坛会的了解情况为“非常了解”的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生“阳光体育运动”的实施情况,随机调查了40名学生一周的体育锻炼时间,并绘制成了如下图所示的条形统计图,根据统计图提供的数据,该校40名同学一周参加体育锻炼时间的众数与中位数分别是( )
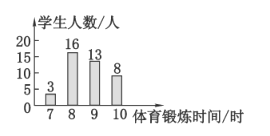
A.8,9B.8,8C.9,8D.10,9
查看答案和解析>>
科目:初中数学 来源: 题型:
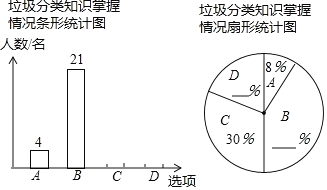
【题目】为响应市政府关于“垃圾不落地市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的掌握情况.调查选项分为“A:非常了解,B:比较了解,C:了解较少,D:不了解”四种,并将调查结果绘制成两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)把两幅统计图补充完整;
(2)若该校学生有2000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有 名;
(3)已知“非常了解”的同学有3名男生和1名女生,从中随机抽取2名进行垃圾分类的知识交流,请用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 为常数,且
为常数,且![]() )中的
)中的![]() 与
与![]() 的部分对应值如表:
的部分对应值如表:
| ··· |
|
|
|
| ··· |
| ··· |
|
|
|
| ··· |
下列结论错误的是( )
A.![]() B.
B.![]() 是关于
是关于![]() 的方程
的方程![]() 的一个根;
的一个根;
C.当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而减小;D.当
值的增大而减小;D.当![]() 时,
时,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、点
、点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,顶点
,顶点![]() 的横坐标为
的横坐标为![]() ,对称轴交
,对称轴交![]() 轴交于点
轴交于点![]() ,交
,交![]() 与点
与点![]() .
.
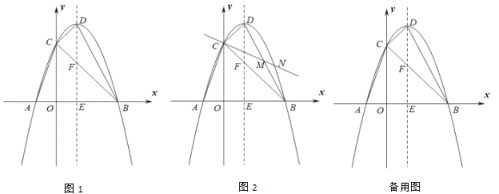
(1)求顶点![]() 的坐标;
的坐标;
(2)如图2所示,过点![]() 的直线交直线
的直线交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .
.
①若直线![]() 将
将![]() 分成的两部分面积之比为
分成的两部分面积之比为![]() ,求点
,求点![]() 的坐标;
的坐标;
②若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
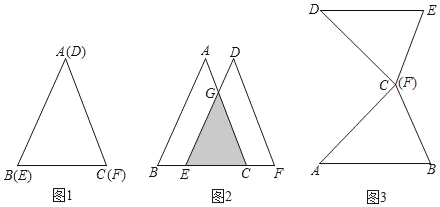
【题目】如图1,已知三角形纸片△ABC和△DEF重合在一起,AB=AC,DE=DF,△ABC≌△DEF.数学实验课上,张老师让同学们用这两张纸片进行如下操作:
(1)(操作探究1)保持△ABC不动,将△DEF沿射线BC方向平移至图2所示位置,通过度量发现BE:CE=1:2,则S△CGE:S△CAB= ;
(2)(操作探究2)保持△ABC不动,将△DEF通过一次全等变换(平移、旋转或翻折后和△ABC拼成以BC为一条对角线的菱形,请用语言描述你的全等变换过程.
(3)(操作探究3)将两个三角形按图3所示放置:点C与点F重合,AB∥DE.保持△ABC不动,将△DEF沿射线DA方向平移.若AB=13,BC=10,设△DEF平移的距离为m.
①当m=0时,连接AD、BE,判断四边形ABED的形状并说明理由;
②在平移的过程中,四边形ABED能否成为正方形?若能,请求出m的值;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com