
【题目】为了解学生对博鳌论坛会的了解情况,某中学随机抽取了部分学生进行问卷调查,将调查结果记作“![]() 非常了解,
非常了解,![]() 了解,
了解,![]() 了解较少,
了解较少,![]() 不了解.”四类分别统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
不了解.”四类分别统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
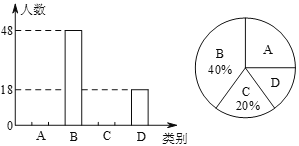
(1)此次共调查了______名学生;扇形统计图中![]() 所在的扇形的圆心角度数为______;
所在的扇形的圆心角度数为______;
(2)将条形统计图补充完整;
(3)若该校共有1600名学生,请你估计对博鳌论坛会的了解情况为“非常了解”的学生约有多少人?
【答案】(1)120;54°;(2)补图见解析;(3) 400人.
【解析】
(1)由B类别人数及其所占百分比可得;用总人数乘以D类别人数占总人数的比例即可得;
(2)先用总人数乘以C类别的百分比求得其人数,再根据各类别百分比之和等于总人数求得A的人数即可补全图形;
(3)用总人数乘以样本中A类别的人数所占比例即可得.
(1)本次调查的总人数为48÷40%=120(名),
扇形统计图中D所在的扇形的圆心角为360°×![]() =54°,
=54°,
故答案为120;54°;
(2)C类别人数为120×20%=24(人),
则A类别人数为120﹣(48+24+18)=30(人),
补全条形图如下:
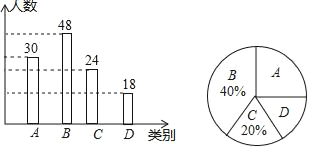
(3)估计对文明城市的了解情况为“非常了解”的学生的人数为1600×![]() =400(人).
=400(人).
答:该校对博鳌论坛会的了解情况为“非常了解”的学生约有400人.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】(发现问题)
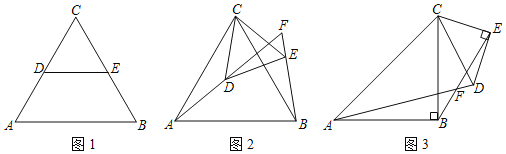
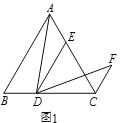
(1)如图1,已知△CAB和△CDE均为等边三角形,D在AC上,E在CB上,易得线段AD和BE的数量关系是 .
(2)将图1中的△CDE绕点C旋转到图2的位置,直线AD和直线BE交于点F.
①判断线段AD和BE的数量关系,并证明你的结论;
②图2中∠AFB的度数是 .
(探究拓展)
(3)如图3,若△CAB和△CDE均为等腰直角三角形,∠ABC=∠DEC=90°,AB=BC,DE=EC,直线AD和直线BE交于点F,分别写出∠AFB的度数,线段AD、BE间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
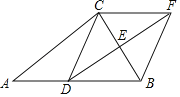
【题目】在Rt△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,过点C作CF∥AB,与DE的延长线并交于点F,连接BF.
(1)试判断四边形CDBF的形状,并说明理由;
(2)若CD=5,sin∠CAB=![]() ,过点C作CH⊥BF,垂足为H点,试求CH的长.
,过点C作CH⊥BF,垂足为H点,试求CH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
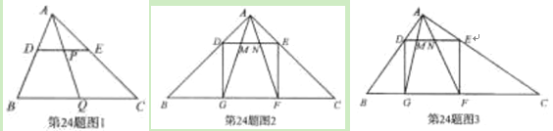
【题目】(本题满分10分)(1)如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P.求证:![]() .
.
(2)如图,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长;
②如图3,求证MN2=DM·EN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把有一组对角为直角的四边形叫直方形.设这两个直角的夹边长分别为a,b和c,d,记![]() 叫直方形的方周长,如图1.
叫直方形的方周长,如图1.
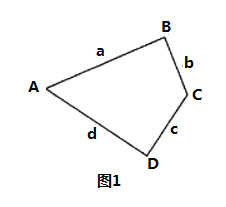

(1)判断![]() 与
与![]() 的大小;
的大小;
(2)如图2,已知点P为双曲线![]()
![]() 上一动点,过点P作PA⊥x轴交x轴正半轴于点A,以坐标原点O为圆心、OA长为半径作
上一动点,过点P作PA⊥x轴交x轴正半轴于点A,以坐标原点O为圆心、OA长为半径作![]() ,点B为
,点B为![]() 上不同于点A的点,当以点P,A,O,B为顶点的直方形的方周长
上不同于点A的点,当以点P,A,O,B为顶点的直方形的方周长![]() 取最小值时,求直方形PAOB的面积;
取最小值时,求直方形PAOB的面积;
(3)已知直线![]() :
:![]() 与x轴、y轴相交于点A,B,点P为平面上一点,以点P,A,O,B为顶点的直方形的方周长
与x轴、y轴相交于点A,B,点P为平面上一点,以点P,A,O,B为顶点的直方形的方周长![]() ,当反比例函数
,当反比例函数![]() 的图象与直线
的图象与直线![]() 有两个交点时,求k的取值范围.
有两个交点时,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,在等边![]() 中,点
中,点![]() 为
为![]() 边上一动点,
边上一动点,![]() 交
交![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() .则
.则![]() 与
与![]() 的数量关系是_____,
的数量关系是_____,![]() 的度数为______.
的度数为______.
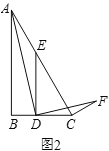
(2)拓展探究:如图2,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一动点,
边上一动点,![]() 交
交![]() 于点
于点![]() ,当∠ADF=∠ACF=90°时,求
,当∠ADF=∠ACF=90°时,求![]() 的值.
的值.
(3)解决问题:如图3,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的延长线上一点,过点
的延长线上一点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,直接写出当
,直接写出当![]() 时
时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读以下材料,并完成相应任务:
斐波那契(约1170-1250)是意大利数学家.1202年,撰写了《算盘书》一书,他是第一个研究了印度和阿拉伯数学理论的欧洲人,他还曾在埃及、叙利亚、希腊,以及意大利西西里和法国普罗旺斯等地研究数学.他研究了一列非常奇妙的数:0,1,1,2,3,5,8,13,21,34,55,89,144……这列数,被称为斐波那契数列.其特点是从第3项开始,每一项都等于前两项之和,斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.

任务:(1)填写下表并写出通过填表你发现的规律:
项 | 第2项 | 第3项 | 第4项 | 第5项 | 第6项 | 第7项 | 第8项 | 第9项 | … |
这一项的平方 | 1 | 1 | 4 | 9 | 25 | ________ | _______ | 441 | … |
这一项的前、后两项的积 | 0 | 2 | 3 | 10 | 24 | _______ | _______ | 442 | … |
规律:_____________;
(2)现有长为![]() 的铁丝,要截成
的铁丝,要截成![]() 小段,每段的长度不小于
小段,每段的长度不小于![]() ,如果其中任意三小段都不能拼成三角形,则
,如果其中任意三小段都不能拼成三角形,则![]() 的最大值为___________________.
的最大值为___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提升学生的艺术素养,学校计划开设四门艺术选修课:A.书法;B.绘画;C.乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
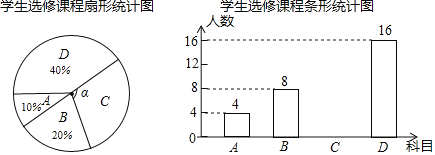
(1)本次调查的学生共有多少人?扇形统计图中∠α的度数是多少?
(2)请把条形统计图补充完整;
(3)学校为举办2018年度校园文化艺术节,决定从A.书法;B.绘画;C.乐器;D.舞蹈四项艺术形式中选择其中两项组成一个新的节目形式,请用列表法或树状图求出选中书法与乐器组合在一起的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com