
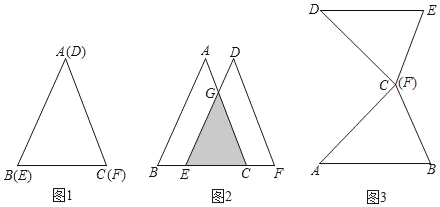
【题目】如图1,已知三角形纸片△ABC和△DEF重合在一起,AB=AC,DE=DF,△ABC≌△DEF.数学实验课上,张老师让同学们用这两张纸片进行如下操作:
(1)(操作探究1)保持△ABC不动,将△DEF沿射线BC方向平移至图2所示位置,通过度量发现BE:CE=1:2,则S△CGE:S△CAB= ;
(2)(操作探究2)保持△ABC不动,将△DEF通过一次全等变换(平移、旋转或翻折后和△ABC拼成以BC为一条对角线的菱形,请用语言描述你的全等变换过程.
(3)(操作探究3)将两个三角形按图3所示放置:点C与点F重合,AB∥DE.保持△ABC不动,将△DEF沿射线DA方向平移.若AB=13,BC=10,设△DEF平移的距离为m.
①当m=0时,连接AD、BE,判断四边形ABED的形状并说明理由;
②在平移的过程中,四边形ABED能否成为正方形?若能,请求出m的值;若不能,请说明理由.
【答案】(1)4:9;(2)将△DEF沿EF翻折或绕BC中点旋转180°;(3)①矩形,理由见解析;②能,m=![]() 或m=
或m=![]() .
.
【解析】
(1)证△CGE∽△CAB,得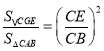 ;(2)运用翻折或旋转;(3)①先证四边形ABED是平行四边形,再证四边形ABED是矩形;②过点A作AG⊥BC,过点C作CH⊥BE,CM⊥AB,根据勾股定理求出AG,再求出三角形ABC的面积,得BH=CM=
;(2)运用翻折或旋转;(3)①先证四边形ABED是平行四边形,再证四边形ABED是矩形;②过点A作AG⊥BC,过点C作CH⊥BE,CM⊥AB,根据勾股定理求出AG,再求出三角形ABC的面积,得BH=CM=![]() ,BE=2BH=
,BE=2BH=![]() ,根据平移定义得BE=AB.
,根据平移定义得BE=AB.
(1)如图2,由题意知DE∥AB,
∴△CGE∽△CAB,
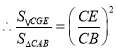
![]()
![]()
则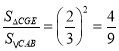
故答案为:4:9;
(2)将△DEF沿EF翻折或绕BC中点旋转180°;
(3)①∵AB∥DE且AB=BC=DC=DE,
∴四边形ABED是平行四边形,
∵∠DEC+∠CEB+∠CBE+∠ABC=180°,
且∠DEC=∠ABC,∠CEB=∠CBE,
∴∠DEC+∠CEB=90°,即∠BED=90°,
∴四边形ABED是矩形;
②能,
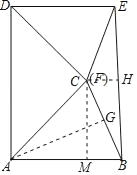
如图,过点A作AG⊥BC,过点C作CH⊥BE,CM⊥AB,
![]()
![]()
![]() ∴CM=
∴CM=![]() ,
,
则BH=CM=![]() ,BE=2BH=
,BE=2BH=![]() ,
,
∵四边形ABED是正方形,
∴平移后BE=AB,
则m=![]() 或m=
或m=![]() .
.


科目:初中数学 来源: 题型:
【题目】请阅读以下材料,并完成相应任务:
斐波那契(约1170-1250)是意大利数学家.1202年,撰写了《算盘书》一书,他是第一个研究了印度和阿拉伯数学理论的欧洲人,他还曾在埃及、叙利亚、希腊,以及意大利西西里和法国普罗旺斯等地研究数学.他研究了一列非常奇妙的数:0,1,1,2,3,5,8,13,21,34,55,89,144……这列数,被称为斐波那契数列.其特点是从第3项开始,每一项都等于前两项之和,斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.

任务:(1)填写下表并写出通过填表你发现的规律:
项 | 第2项 | 第3项 | 第4项 | 第5项 | 第6项 | 第7项 | 第8项 | 第9项 | … |
这一项的平方 | 1 | 1 | 4 | 9 | 25 | ________ | _______ | 441 | … |
这一项的前、后两项的积 | 0 | 2 | 3 | 10 | 24 | _______ | _______ | 442 | … |
规律:_____________;
(2)现有长为![]() 的铁丝,要截成
的铁丝,要截成![]() 小段,每段的长度不小于
小段,每段的长度不小于![]() ,如果其中任意三小段都不能拼成三角形,则
,如果其中任意三小段都不能拼成三角形,则![]() 的最大值为___________________.
的最大值为___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
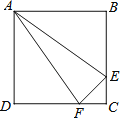
A. 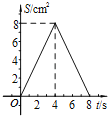 B.
B. 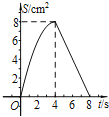
C. 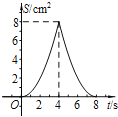 D.
D. 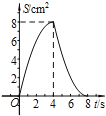
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提升学生的艺术素养,学校计划开设四门艺术选修课:A.书法;B.绘画;C.乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
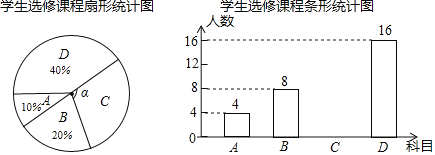
(1)本次调查的学生共有多少人?扇形统计图中∠α的度数是多少?
(2)请把条形统计图补充完整;
(3)学校为举办2018年度校园文化艺术节,决定从A.书法;B.绘画;C.乐器;D.舞蹈四项艺术形式中选择其中两项组成一个新的节目形式,请用列表法或树状图求出选中书法与乐器组合在一起的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生使用手机情况,随机抽取了部分学生进行|使用手机的目的和每周使用手机的时间的问卷调查,并绘制成如图所示的统计图,已知“查资料”的人数为38人。
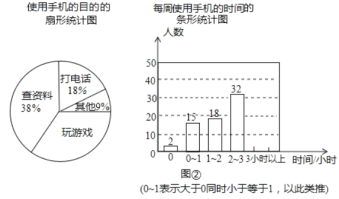
根据以上信息,回答下列问题:
(1)这次调查中,一共抽查了__________名学生;
(2)在扇形统计图中,“玩游戏”所对应的圆心角的度数是___________度;
(3)补全条形统计图;
(4)若该校共有学生2000人,请你估计每周使用手机时间超过2小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根调查结果绘制成的统计图(部分)如图所示.
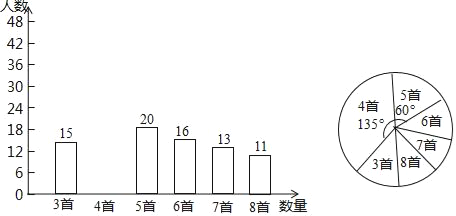
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 10 | 10 | 15 | 40 | 25 | 20 |
请根据调查的信息
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过点A,连接AE、CF相交于点P.将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°的过程中,线段OP的最小值为_____.
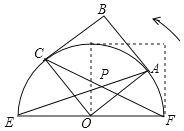
查看答案和解析>>
科目:初中数学 来源: 题型:
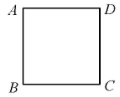
【题目】数学课上,王老师让同学们对给定的正方形![]() ,建立合适的平面直角坐标系,并表示出各顶点的坐标.下面是4名同学表示各顶点坐标的结果:
,建立合适的平面直角坐标系,并表示出各顶点的坐标.下面是4名同学表示各顶点坐标的结果:
甲同学:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
乙同学:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
丙同学:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
丁同学:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
上述四名同学表示的结果中,四个点的坐标都表示正确的同学是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按![]() 元销售时,每天可销售
元销售时,每天可销售![]() 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出![]() 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为![]() 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润![]() 元?
元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com