
����Ŀ���ó���һ���IJ���ֲ�����Ƴ����Ϊ���εĿ�ܣ���ͼ�٢��е�һ�֣���������AB=x�ף����������ͼ���ش��������⣺�����еIJ���ֲ����ܳ���ָ��ͼ�����к��ߵij��Ⱥͣ����кᵵ�������ֱ���AD��ABƽ�У�
��1����ͼ���У��������ֲ����ܳ���Ϊ12�ף���xΪ����ʱ�����ο��ABCD�����Ϊ3ƽ���ף�
��2����ͼ���У��������ֲ����ܳ���Ϊ12�ף���xΪ����ʱ�����ο��ABCD�����S����������Ƕ��٣�
���𰸡�
��1���⣺�����⣬BC�ij�Ϊ(4x)�ף������⣬�ã�
x(4x)=3����x4x+3=0����� x1=1��x2=3��
�𣺵�AB�ij���Ϊ1��3��ʱ�����ο��ABCD�����Ϊ3ƽ���ף�
��2���⣺�������⣬��ͼ2�ã�AD=(124x)��3=4 ![]() x����S=ABAD=x(4
x����S=ABAD=x(4 ![]() x)=
x)= ![]() x+4x
x+4x
�䷽��S= ![]() ���൱x=
���൱x= ![]() ʱ��Sȡ���ֵ3��
ʱ��Sȡ���ֵ3��
�𣺵�x= ![]() ʱ�����ο��ABCD����������������3ƽ���ף�
ʱ�����ο��ABCD����������������3ƽ���ף�
����������1������ͼ�ο�֪AB+BC=4�����ú�x�Ĵ���ʽ��ʾ��BC�ij���Ȼ����ݾ��ε������ʽ�������̣���⼴�ɡ�
��2������ͼ�ڿ�֪4AB+3BC=12���ú�x�Ĵ���ʽ��ʾ��AD�ij����ٸ���S=ABAD������s��x�ĺ�����ϵʽ��Ȼ������������꣬������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��һԪ���η���
��һԪ���η���![]() ������ʵ����
������ʵ����![]() ��
��![]() ��
��
��1����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̼��������ɫ���С�������õ����Ⱥ�ڵĽ��ܣ�Խ��Խ������ٴ�ѡ�����г���Ϊ���й��ߣ�С���Ͱְ�ͬʱ�Ӽ������г�ȥͼ��ݣ��ְ�����150��/�ֵ��ٶ�����һ��ʱ�䣬��Ϣ��5���ӣ�����m��/�ֵ��ٶȵ���ͼ��ݣ�С��ʼ����ͬһ�ٶ����У�������ʻ��·��y���ף���ʱ��x�����ӣ��Ĺ�ϵ��ͼ������ͼ����������⣺ 
��1��a= �� b= �� m= ��
��2����С�����ٶ���120��/�֣���С����;����ְֵڶ�������ʱ����ͼ��ݵľ��룻
��3���ڣ�2���������£��ְ��Եڶ��γ���������ͼ���ǰ����ʱ��С�����100�ף�
��4����С������ʻ�ٶ���v��/�֣�����;����ְ�ǡ���������Σ��������ҡ�ͼ������أ�����ֱ��д��v��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��EF ��ƽ���ı��� ABCD �Խ��ߵĽ��� O���� AD �� E���� BC �� F����ƽ���ı��� ABCD ���ܳ�Ϊ32��OE��2�����ı��� ABFE ���ܳ�Ϊ__________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı��� ABCD �ĶԽ��� AC��BD ���� O �㣬AE��BD����AED����AOD������ OE��

��1����֤��AE��OB��
��2����֤���ı��� CDEO ��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ���飩
��1���ⲻ��ʽ![]() ��1�����������ϱ�ʾ���Ľ⼯��
��1�����������ϱ�ʾ���Ľ⼯��
![]()
��2���ⲻ��ʽ�� ��������������зǸ�������֮�ͣ�
��������������зǸ�������֮�ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ߵĶ�����ͬ���������Ϊ���Ѻ������ߡ���������C1��y1=��2x2+4x+2��C2��u2=��x2+mx+nΪ���Ѻ������ߡ���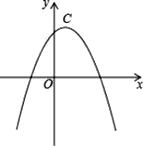
��1����������C2�Ľ���ʽ��
��2����A��������C2���ڵ�һ���Ķ��㣬��A��AQ��x�ᣬQΪ���㣬��AQ+OQ�����ֵ��
��3����������C2�Ķ���ΪC����B������Ϊ����1��4��������C2�ĶԳ������Ƿ���ڵ�M��ʹ�߶�MB�Ƶ�M��ʱ����ת90��õ��߶�MB�䣬�ҵ�B��ǡ������������C2�ϣ������������M�����꣬������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽƬABCD�У�AD=4cm����ֽƬ��ֱ��AC�۵�����B����E����AE��DC�ڵ�O����AO=5cm����AB�ij�Ϊ�� �� 
A.6cm
B.7cm
C.8cm
D.9cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������AOCD��ֱ��AE�۵�����E�ڱ�DC�ϣ����۵���˵�Dǡ�����ڱ�OC�ϵĵ�F��������D������Ϊ��10��8�������E������Ϊ .
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com