
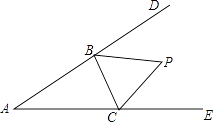
【题目】如图,在△ABC中,分别延长△ABC的边AB,AC到D,E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业时发现如下规律: a.若∠A=50°,则∠P=65°=90°﹣ ![]() ;
;
b.若∠A=90°,则∠P=45°=90°﹣ ![]() ;
;
c.若∠A=100°,则∠P=40°=90°﹣ ![]() ;
;
(1)根据上述规律,若∠A=150°,则∠P=;
(2)请你用数学表达式归纳出∠P与∠A的关系;
(3)请说明你的结论.
【答案】
(1)解:15°
(2)解:∠P与∠A的关系为∠P=90°﹣ ![]() ∠A
∠A
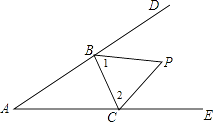
(3)解:理由如下:
如图,
∵∠CBD与∠BCE的平分线相交于点P,
∴∠1= ![]() ∠DBC,∠2=
∠DBC,∠2= ![]() ∠BCE,
∠BCE,
∵∠P=180°﹣∠1﹣∠2=180°﹣ ![]() (∠DBC+∠BCE),
(∠DBC+∠BCE),
而∠DBC=180°﹣∠ABC,∠BCE=180°﹣∠ACB,
∴∠P=180°﹣ ![]() (180°﹣∠ABC+180°﹣∠ACB)
(180°﹣∠ABC+180°﹣∠ACB)
= ![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
而∠ABC+∠ACB=180°﹣∠A,
∴∠P= ![]() (180°﹣∠A)=90°﹣
(180°﹣∠A)=90°﹣ ![]() ∠A.
∠A.
【解析】解:(1)若∠A=150°,则∠P=90°﹣ ![]() =15°;所以答案是15°;
=15°;所以答案是15°;
【考点精析】利用三角形的内角和外角对题目进行判断即可得到答案,需要熟知三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】植树节期间,某单位欲购进A、B两种树苗,若购进A种树苗3棵,B种树苗5棵,需2100元,若购进A种树苗4棵,B种树苗10棵,需3800元.
(1)求购进A、B两种树苗的单价;
(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵,求A种树苗至少需购进多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,每个圆周上的数是按下述规则逐次标出的:第一次先在圆周上标出0,1两个数(如图1);第二次又在第一次标出的两个数之间的圆周上,分别标出这两个数的和(图2);第三次再在第二次标出的所有相邻两数之间的圆周上,分别标出相邻两数的和(如图3).按此规则以此类推,第2013次标完数字后,圆周上所有数字的和S2013= . 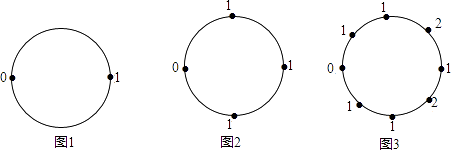
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校到学习基地的公路距离为15千米,一部分人骑自行车先走,40分钟后,其余的人乘坐汽车出发,结果他们同时到达,如果汽车的平均速度与自行车的平均速度的比是3:1,问:汽车与自行车的平均速度分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com