
【题目】如图,已知A(﹣2,4),B(4,2),C(2,﹣1)
(1)作△ABC关于x轴的对称图形△A1B1C1,写出点C关于x轴的对称点C1的坐标;
(2)P为x轴上一点,请在图中画出使△PAB的周长最小时的点P并直接写出此时点P的坐标(保留作图痕迹).
【答案】详见解析.
【解析】试题分析:
(1) 先根据题目给出的已知点的坐标,在图中的相应位置上标出原三角形的三个顶点. 根据关于x轴对称的点的坐标规律,将对称变换后的三角形的顶点坐标写出,即A1 (-2, -4),B1 (4, -2),C1 (2, 1). 在图中相应的位置上标出对称变换后的三角形的三个顶点. 连接这三个顶点即得所求的△A1B1C1. 至于题目中有关写出点C1坐标的问题,可以根据前面得到的点C1的坐标作答即可.
(2) △PAB的周长为PA+PB+AB. 由于点A和点B均为坐标已知的固定点,所以线段AB的长度是一个定值. 因此,△PAB的周长最小就是PA+PB最小. 这种最小值问题可以利用轴对称进行求解. 先将点A关于x轴的对称点A1画出:过点A作x轴的垂线(为叙述方便,设垂足为点D),在线段AD的延长线上截取DA1=DA,则点A1即为点A关于x轴的对称点. 然后,连接A1B,交x轴于点P,则点P即为所求. 观察图形不难看出,点P的坐标为(2, 0).
试题解析:
(1) 如图所示,△A1B1C1即为所求.
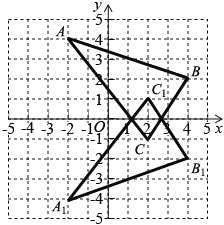
∵点C与点C1关于x轴对称,
又∵点C的坐标为(2, -1),
∴点C1的坐标为(2, 1).
(2) 如图所示,点P即为所求.
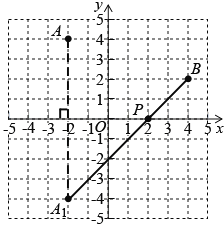
根据上述图形可知,点P的坐标为(2, 0).


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,因为AB∥CD(已知),所以∠BEF=∠CFE(两直线平行,) 因为EG平分∠BEF,FH平分∠CFE(已知),
所以∠2= ![]() ∠BEF,∠3=()
∠BEF,∠3=()
所以∠2=(等量代换),
所以EG∥( , 两直线平行).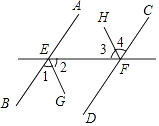
查看答案和解析>>
科目:初中数学 来源: 题型:
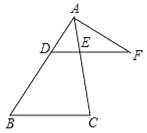
【题目】如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.
(1)如果![]() ,DE=6,求边BC的长;
,DE=6,求边BC的长;
(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
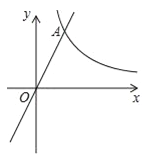
【题目】已知:如图,在平面直角坐标系xOy中,反比例函数![]() 的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.
的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.
(1)求平移后直线的表达式;
(2)求∠OBC的余切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③BC平分∠ABD;④AF=DF;⑤BD=2OF.其中正确结论的个数是( )
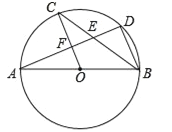
A.2 B.3 C.4 D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com