
【题目】如图,P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足.
(1)求证:△APD≌△CPD;
(2)若CF=3,CE=4,求AP的长.

【答案】(1)证明见解析;(2)5.
【解析】试题分析:
(1)根据正方形的性质,用SAS证明△APD≌△CPD;
(2)证明四边形PEDF是矩形,用勾股定理求EF,结合矩形的性质和(1)的结论求AP的长.
试题解析:
证明:(1)∵四边形ABCD是正方形,
∴AD=CD,∠ADP=∠CDP=45°,∠BCD=90°,
在△APD和△CPD中,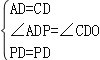 ,
,
∴△APD≌△CPD(SAS);
(2)解:∵△APD≌△CPD,∴AP=PC,
∵四边形ABCD是正方形,∴∠BCD=90°,
∵PE⊥DC,PF⊥BC,∴∠PEC=∠PFC=90°,
∴四边形PECF是矩形,∴PC=EF,∴AP=EF.
∵∠DCB=90°,∴在Rt△CEF中,EF=![]() =
=![]() =5,
=5,
∴AP=EF=5.


科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16.
(1)求C点坐标;
(2)如图2,设D为线段OB上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P,求∠APD的度数.
(3)如图3,当D点在线段OB上运动时,作DM⊥AD交BC于M点,∠BMD、∠DAO的平分线交于N点,则D点在运动过程中,∠N的大小是否变化?若不变,求出其值,若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 厘米,
厘米,![]() ,
,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点,如果点
的中点,如果点![]() 在线段
在线段![]() 上以
上以![]() 厘米/秒的速度由点向点运动,同时点
厘米/秒的速度由点向点运动,同时点![]() 在线段
在线段![]() 上由
上由![]() 点向
点向![]() 点运动.当一个点停止运动时,另一个点也随之停止运动.
点运动.当一个点停止运动时,另一个点也随之停止运动.

(1)用含有![]() 的代数式表示
的代数式表示![]() ,则
,则![]() _______厘米;
_______厘米;
(2)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,经过
的运动速度相等,经过![]() 秒后,
秒后,![]() 与
与![]() 是否全等,请说明理由;
是否全等,请说明理由;
(3)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,那么当点
的运动速度不相等,那么当点![]() 的运动速度为多少时,能够使
的运动速度为多少时,能够使![]() 与
与![]() 全等?
全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
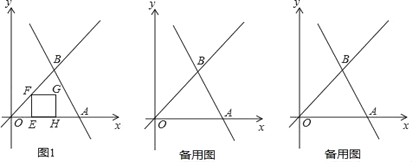
【题目】如图1,直线y=﹣2x+3与x轴交于点A,与直线y=x交于点B.
(1)点A坐标为 ,∠AOB= ;
(2)求S△OAB的值;
(3)动点E从原点O出发,以每秒1个单位长度的速度沿着O→A的路线向终点A匀速运动,过点E作EF⊥x轴交直线y=x于点F,再以EF为边向右作正方形EFGH.设运动t秒时,正方形EFGH与△OAB重叠部分的面积为S.求:S与t之间的函数关系式,并写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.
(1)求∠E的度数.
(2)求证:M是BE的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知 )
∴ (同角的补角相等)①
∴ (内错角相等,两直线平行)②
∴∠ADE=∠3( )③
∵∠3=∠B( )④
∴ (等量代换)⑤
∴DE∥BC( )⑥
∴∠AED=∠C( )⑦

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国流传了上千年的传统节日,全国各地举行了丰富多彩的纪念活动,为了继承传统,减缓学生考前的心理压力,某班学生组织了一次拔河比赛,裁判员让两队队长用“石头、剪刀、布”的手势方式选择场地位置,规则是:石头胜剪刀,剪刀胜布,布胜石头,手势相同则再决胜负.
(1)用列表或画树状图法,列出甲、乙两队手势可能出现的情况;
(2)裁判员的这种做法对甲、乙双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个计算器,计算![]() 时只能显示1.41421356237十三位(包括小数点),现在想知道7后面的数字是什么,可以在这个计算器中计算下面哪一个值( )
时只能显示1.41421356237十三位(包括小数点),现在想知道7后面的数字是什么,可以在这个计算器中计算下面哪一个值( )
A. 10![]() B. 10(
B. 10(![]() -1) C. 100
-1) C. 100![]() D.
D. ![]() -1
-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com