
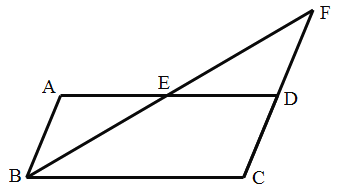
【题目】如图,在□ABCD中,E是AD边上的中点,连接BE并延长交CD的延长线于点F.
(1)证明:FD=AB;
(2)当平行四边形ABCD的面积为8时,求△FED的面积.
【答案】(1)证明见解析
(2)△FED的面积为2.
【解析】
试题(1)根据平行四边形的性质,可知AB//CD,可是∠ABE=∠F,又AE=DE,∠BEA=∠FED由AAS可证明△ABE≌△DFE,可得FD=AB
(2)由AD//BC可得∴△FED∽△FBC,由相似三角形的性质可知S△FED:S△FBC=(FE:FB)2,根据(1)可得BE=EF,S△FDE=S平行四边形ABCD,从而可得△FED的面积为2.
试题解析:(1)∵在平行四边形ABCD中,E是AD边上的中点,∴AE=ED,∠ABE=∠F,
在△ABE和△DFE中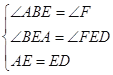 ,∴△ABE≌△DFE(AAS),∴FD=AB;
,∴△ABE≌△DFE(AAS),∴FD=AB;
(2)∵DE∥BC,∴△FED∽△FBC,∵△ABE≌△DFE,
∴BE=EF,S△FDE=S平行四边形ABCD,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴△FED的面积为:2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交BC于点D,且D在以AE为直径的⊙O上.
(1)求证:BC是⊙O的切线;
(2)已知∠B=30°,CD=4,求线段AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,直接写出抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,请用列表法或树状图法,求抽到的都是合格品的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
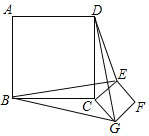
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+b2,其中正确结论是_____(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com