
 如图,?ABCD中,点E、F在直线BD上,连接AF、CE,不添加任何辅助线,请添加一个条件DF=BE,使AF=CE(填一个即可)
如图,?ABCD中,点E、F在直线BD上,连接AF、CE,不添加任何辅助线,请添加一个条件DF=BE,使AF=CE(填一个即可) 科目:初中数学 来源: 题型:填空题
 小强从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:
小强从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
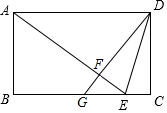 如图,矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE于点F,延长DF交BC于点G,连接DE.
如图,矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE于点F,延长DF交BC于点G,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两车从A地出发匀速行驶至B地,在整个行驶过程中,甲、乙两车离开A地的距离y1(单位:km),y2(单位:km)关于甲车行驶的时间t(单位:h)的函数关系如图所示,根据图象解答下列问题:
甲、乙两车从A地出发匀速行驶至B地,在整个行驶过程中,甲、乙两车离开A地的距离y1(单位:km),y2(单位:km)关于甲车行驶的时间t(单位:h)的函数关系如图所示,根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是40cm.
如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是40cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com