
ЁОЬтФПЁПФГЭцОпЙЋЫОЩњВњвЛжжЕчзгЭцОпЃЌУПжЛЭцОпЕФЩњВњГЩБОЮЊ18дЊЃЌЪдЯњЙ§ГЬжаЗЂЯжЃЌУПдТЯњЪлСПyЃЈЭђжЛЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉжЎМфЕФЙиЯЕПЩвдНќЫЦЕФПДзївЛДЮКЏЪ§y=2x+100ЃЌЩшУПдТЯњЪлетжжЭцОпЕФРћШѓЮЊw(ЭђдЊ).
ЃЈ1ЃЉаДГіwгыxжЎМфЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЕБЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌЙЋЫОУПдТЛёЕУЕФРћШѓЮЊ440ЭђдЊЃП
ЃЈ3ЃЉШчЙћЙЋЫОУПдТЕФЩњВњГЩБОВЛГЌЙ§540ЭђдЊЃЌФЧУДЕБЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌЙЋЫОУПдТЛёЕУЕФРћШѓзюДѓЃПзюДѓРћШѓЮЊЖрЩйЭђдЊЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ ЫљвдЕБЯњЪлЕЅМлЮЊ28дЊЛђ40дЊЪБЃЌЙЋЫОУПдТЛёЕУЕФРћШѓЮЊ440ЭђдЊЃЛЃЈ3ЃЉЕБЯњЪлЕЅМлЮЊ35дЊЪБЃЌЙЋЫОУПдТЛёЕУЕФРћШѓзюДѓЃЌзюДѓРћШѓЮЊ510ЭђдЊ
ЃЛЃЈ2ЃЉ ЫљвдЕБЯњЪлЕЅМлЮЊ28дЊЛђ40дЊЪБЃЌЙЋЫОУПдТЛёЕУЕФРћШѓЮЊ440ЭђдЊЃЛЃЈ3ЃЉЕБЯњЪлЕЅМлЮЊ35дЊЪБЃЌЙЋЫОУПдТЛёЕУЕФРћШѓзюДѓЃЌзюДѓРћШѓЮЊ510ЭђдЊ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнРћШѓ=УПжЛЭцОпЕФРћШѓЁСЯњЪлСПМДПЩЕУЕНwгыxжЎМфЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉСюЕкЃЈ1ЃЉЮЪжаЕФwЕШгк440ЃЌНЈСЂвЛИіЙигкxЕФвЛдЊЖўДЮЗНГЬЃЌНтЗНГЬМДПЩЃЛ
ЃЈ3ЃЉЯШЭЈЙ§УПдТЕФЩњВњГЩБОВЛГЌЙ§540ЭђдЊЧѓГіЕЅМлxЕФЗЖЮЇЃЌШЛКѓдкИУЗЖЮЇФкЧѓwЕФзюДѓжЕМДПЩ.
ЃЈ1ЃЉИљОнЬтвтга![]()
ЃЈ2ЃЉСю![]()
НтЕУ![]()
ЫљвдЕБЯњЪлЕЅМлЮЊ28дЊЛђ40дЊЪБЃЌЙЋЫОУПдТЛёЕУЕФРћШѓЮЊ440ЭђдЊ
ЃЈ3ЃЉЁпУПдТЕФЩњВњГЩБОВЛГЌЙ§540ЭђдЊЃЌУПжЛЭцОпЕФЩњВњГЩБОЮЊ18дЊ
ЁрУПдТЕФЩњВњСП![]()
МД![]()
НтЕУ![]()
гжЁп![]()
Ёр![]()
Ёр![]()
Ёп![]()
ЁрЭМЯѓПЊПкЯђЯТЃЌЕБ![]() ЪБЃЌwЫцзХxЕФдіДѓЖјМѕаЁ
ЪБЃЌwЫцзХxЕФдіДѓЖјМѕаЁ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЭђдЊ
ЭђдЊ
ЫљвдЕБЯњЪлЕЅМлЮЊ35дЊЪБЃЌЙЋЫОУПдТЛёЕУЕФРћШѓзюДѓЃЌзюДѓРћШѓЮЊ510ЭђдЊ


 ЕМбЇШЋГЬСЗДДгХбЕСЗЯЕСаД№АИ
ЕМбЇШЋГЬСЗДДгХбЕСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкRt![]() жаЃЌЁЯA=90ЁуЃЌAC=4ЃЌ
жаЃЌЁЯA=90ЁуЃЌAC=4ЃЌ![]() ЃЌНЋ
ЃЌНЋ![]() бизХаББпBCЗелЃЌЕуAТфдкЕу
бизХаББпBCЗелЃЌЕуAТфдкЕу![]() ДІЃЌЕуDЁЂEЗжБ№ЮЊБпACЁЂBCЕФжаЕуЃЌСЊНсDEВЂбгГЄНЛ
ДІЃЌЕуDЁЂEЗжБ№ЮЊБпACЁЂBCЕФжаЕуЃЌСЊНсDEВЂбгГЄНЛ![]() ЫљдкжБЯпгкЕуFЃЌСЊНс
ЫљдкжБЯпгкЕуFЃЌСЊНс![]() ЃЌШчЙћ
ЃЌШчЙћ![]() ЮЊжБНЧШ§НЧаЮЪБЃЌФЧУД
ЮЊжБНЧШ§НЧаЮЪБЃЌФЧУД![]() ____________
____________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЕу
жаЃЌЕу![]() ЃЌЕу
ЃЌЕу![]() .
.
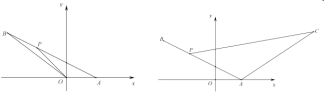
ЃЈ1ЃЉЧѓжБЯп![]() ЕФКЏЪ§БэДяЪНЃЛ
ЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯЕФвЛЕуЃЌЕБ
ЩЯЕФвЛЕуЃЌЕБ![]() ЪБЃЌЧѓЕу
ЪБЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌНЋЯпЖЮ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЃЌЕу
ЃЌЕу![]() ТфдкЕу
ТфдкЕу![]() ДІЃЌСЌНс
ДІЃЌСЌНс![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§ЃЌВЂжБНгаДГіЕу
ЕФУцЛ§ЃЌВЂжБНгаДГіЕу![]() ЕФзјБъ.
ЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
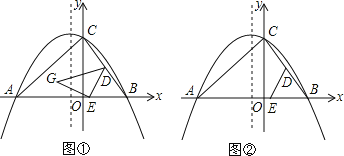
ЁОЬтФПЁПвбжЊЃЌЁїABCдкЦНУцжБНЧзјБъЯЕжаЕФЮЛжУШчЭМЂйЫљЪОЃЌAЕузјБъЮЊЃЈЉ6ЃЌ0ЃЉЃЌBЕузјБъЮЊЃЈ4ЃЌ0ЃЉЃЌЕуDЮЊBCЕФжаЕуЃЌЕуEЮЊЯпЖЮABЩЯвЛЖЏЕуЃЌСЌНгDEОЙ§ЕуAЁЂBЁЂCШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЮЊyЃНax2+bx+8ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМЂйЃЌНЋЁїBDEвдDEЮЊжсЗелЃЌЕуBЕФЖдГЦЕуЮЊЕуGЃЌЕБЕуGЧЁКУТфдкХзЮяЯпЕФЖдГЦжсЩЯЪБЃЌЧѓGЕуЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМЂкЃЌЕБЕуEдкЯпЖЮABЩЯдЫЖЏЪБЃЌХзЮяЯпyЃНax2+bx+8ЕФЖдГЦжсЩЯЪЧЗёДцдкЕуFЃЌЪЙЕУвдCЁЂDЁЂEЁЂFЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпЕФЖЅЕуЮЊAЃЈ1ЃЌ4ЃЉЃЌХзЮяЯпгыyжсНЛгкЕуBЃЈ0ЃЌ3ЃЉЃЌгыxжсНЛгкCЁЂDСНЕуЃЎЕуPЪЧxжсЩЯЕФвЛИіЖЏЕуЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓCЁЂDСНЕузјБъМАЁїBCDЕФУцЛ§ЃЛ
ЃЈ3ЃЉШєЕуPдкxжсЩЯЗНЕФХзЮяЯпЩЯЃЌТњзуSЁїPCD=![]() SЁїBCDЃЌЧѓЕуPЕФзјБъЃЎ
SЁїBCDЃЌЧѓЕуPЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
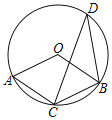
ЁОЬтФПЁПШчЭМЃЌOAЁЂOBЪЧЁбOЕФСНЬѕАыОЖЃЌЁЯAOBЃН120ЁуЃЌЕуCЮЊСгЛЁABЕФжаЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮOACBЮЊСтаЮЃЛ
ЃЈ2ЃЉЕуDЮЊгХЛЁABЩЯвЛЕуЃЌШєЁЯBCDЃНЁЯOBDЃЌBDЃН2ЃЌЧѓOBЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭЌЪБХзжРAЁЂBСНИіОљдШЕФаЁСЂЗНЬхЃЈУПИіУцЩЯЗжБ№БъгаЪ§зж1ЃЌ2ЃЌ3ЃЌ4ЃЌ5ЃЌ6ЃЉЃЌЩшСНСЂЗНЬхГЏЩЯЕФЪ§зжЗжБ№ЮЊxЁЂyЃЌВЂвдДЫШЗЖЈЕуPЃЈxЃЌyЃЉЃЌФЧУДЕуPТфдкХзЮяЯп![]() ЩЯЕФИХТЪЮЊЃЈ ЃЉ
ЩЯЕФИХТЪЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпЕФЖЅЕуЮЊA(1ЃЌ4)ЃЌХзЮяЯпгыyжсНЛгкЕуB(0ЃЌ3)ЃЌгыxжсНЛгкCЁЂDСНЕу.ЕуPЪЧxжсЩЯЕФвЛИіЖЏЕу.
(1)ЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
(2)ЕБPA+PBЕФжЕзюаЁЪБЃЌЧѓЕуPЕФзјБъ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЕу
ЃЎЕу![]() ЪЧЦНУцФкВЛгыЕу
ЪЧЦНУцФкВЛгыЕу![]() ЃЌ
ЃЌ![]() жиКЯЕФШЮвтвЛЕуЃЎСЌНг
жиКЯЕФШЮвтвЛЕуЃЎСЌНг![]() ЃЌНЋЯпЖЮ
ЃЌНЋЯпЖЮ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЕУЕНЯпЖЮ
ЕУЕНЯпЖЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
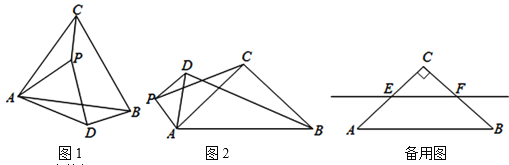
ЃЈ1ЃЉЙлВьВТЯы
ШчЭМ1ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФжЕЪЧ______ЃЌжБЯп
ЕФжЕЪЧ______ЃЌжБЯп![]() гыжБЯп
гыжБЯп![]() ЯрНЛЫљГЩЕФНЯаЁНЧЕФЖШЪ§ЪЧ____________ЃЎЃЈЬсЪОЃКЧѓНЧЖШЪБПЩПМТЧбгГЄ
ЯрНЛЫљГЩЕФНЯаЁНЧЕФЖШЪ§ЪЧ____________ЃЎЃЈЬсЪОЃКЧѓНЧЖШЪБПЩПМТЧбгГЄ![]() НЛ
НЛ![]() ЕФбгГЄЯпгк
ЕФбгГЄЯпгк![]() ЃЉ
ЃЉ
ЃЈ2ЃЉРрБШЬНОП
ШчЭМ2ЃЌЕБ![]() ЪБЃЌЧыаДГі
ЪБЃЌЧыаДГі![]() ЕФжЕМАжБЯп
ЕФжЕМАжБЯп![]() гыжБЯп
гыжБЯп![]() ЯрНЛЫљГЩЕФаЁНЧЕФЖШЪ§ЃЌВЂОЭЭМ2ЕФЧщаЮЫЕУїРэгЩЃЎ
ЯрНЛЫљГЩЕФаЁНЧЕФЖШЪ§ЃЌВЂОЭЭМ2ЕФЧщаЮЫЕУїРэгЩЃЎ
ЃЈ3ЃЉНтОіЮЪЬт
ЕБ![]() ЪБЃЌШєЕу
ЪБЃЌШєЕу![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌЧыжБНгаДГіЕу
ЩЯЃЌЧыжБНгаДГіЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() дкЭЌвЛжБЯпЩЯЪБ
дкЭЌвЛжБЯпЩЯЪБ![]() ЕФжЕ_______________ЃЎ
ЕФжЕ_______________ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com