
【题目】已知如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与点A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)△APD能否构成直角三角形?若能请直接写出点P坐标,若不能请说明理由;
(4)在抛物线对称轴上是否存在点M使|MA﹣MC|最大?若存在请求出点M的坐标,若不存在请说明理由.
【答案】
(1)
解:∵抛物线y=x2+bx+c过点A(3,0),B(1,0),
∴ ![]() ,
,
解得 ![]() ,
,
∴抛物线解析式为y=x2﹣4x+3
(2)
解:令x=0,则y=3,
∴点C(0,3),
则直线AC的解析式为y=﹣x+3,
设点P(x,x2﹣4x+3),
∵PD∥y轴,
∴点D(x,﹣x+3),
∴PD=(﹣x+3)﹣(x2﹣4x+3)=﹣x2+3x=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
∵a=﹣1<0,
∴当x= ![]() 时,线段PD的长度有最大值
时,线段PD的长度有最大值 ![]()
(3)
解:如图
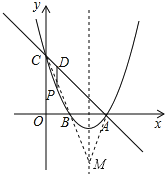
①∠APD是直角时,点P与点B重合,
此时,点P(1,0),
②∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的顶点坐标为(2,﹣1),
∵A(3,0),
∴点P为在抛物线顶点时,∠PAD=45°+45°=90°,
此时,点P(2,﹣1),
综上所述,点P(1,0)或(2,﹣1)时,△APD能构成直角三角形
(4)
解:由抛物线的对称性,对称轴垂直平分AB,
∴MA=MB,
由三角形的三边关系,|MA﹣MC|<BC,
∴当M、B、C三点共线时,|MA﹣MC|最大,为BC的长度,
设直线BC的解析式为y=kx+b(k≠0),
则 ![]() ,
,
解得 ![]() ,
,
∴直线BC的解析式为y=﹣3x+3,
∵抛物线y=x2﹣4x+3的对称轴为直线x=2,
∴当x=2时,y=﹣3×2+3=﹣3,
∴点M(2,﹣3),
即,抛物线对称轴上存在点M(2,﹣3),使|MA﹣MC|最大
【解析】(1)把点A、B的坐标代入抛物线解析式,解方程组得到b、c的值,即可得解;(2)求出点C的坐标,再利用待定系数法求出直线AC的解析式,再根据抛物线解析式设出点P的坐标,然后表示出PD的长度,再根据二次函数的最值问题解答;(3)①∠APD是直角时,点P与点B重合,②求出抛物线顶点坐标,然后判断出点P为在抛物线顶点时,∠PAD是直角,分别写出点P的坐标即可;(4)根据抛物线的对称性可知MA=MB,再根据三角形的任意两边之差小于第三边可知点M为直线CB与对称轴交点时,|MA﹣MC|最大,然后利用待定系数法求出直线BC的解析式,再求解即可.


科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校门前正对一条公路,车流量较大,为便于学生安全通过,特建一座人行天桥.如图,是这座天桥的引桥部分示意图,上桥通道由两段互相平行的楼梯AB、CD和一段平行于地面的平台CB构成.已知∠A=37°,天桥高度DH为5.1米,引桥水平跨度AH为8.3米.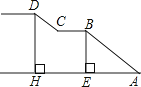
(1)求水平平台BC的长度;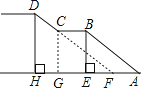
(2)若两段楼梯AB:CD=10:7,求楼梯AB的水平宽度AE的长.
(参考数据:sin37°≈ ![]() ,cos37°≈
,cos37°≈ ![]() ,tan37°≈
,tan37°≈ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑摩托车从邮局出发,先向东骑行2km到达A村,继续向东骑行3km到达B村,然后向西骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用1个单位长度表示1km,请你在数轴上表示出A、B、C三个村庄的位置;
![]()
(2)C村离A村有多远?
(3)若摩托车每1km耗油0.03升,这趟路共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2016次运动后,动点P的坐标是( )
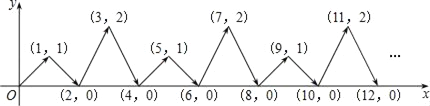
A. (2016,1) B. (2016,0) C. (2016,2) D. (2017,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com