
【题目】组装甲、乙、丙3种产品,需用A、B、C3种零件.每件甲需用A、B各2个;每件乙需用B、C各1个;每件丙需用2个A和1个C.用库存的A、B、C3种零件,如组装成p件甲产品、q件乙产品、r件丙产品,则剩下2个A和1个B,C恰好用完.求证:无论怎样改变生产甲、乙、丙的件数,也不能把库存的A、B、C3种零件都恰好用完.
【答案】解:由已知,库存的A、B、C3种零件的个数分别为:
A种2p+2r+2件,B种2p+q+1件,C种q+r件.
假设生产甲x件,乙y件,丙z件恰好将3种零件都用完,则由题意得:
(1)+(3)﹣(2)得:3z=3r+1它的左边是3的倍数,而右边却是3的倍数加1,矛盾,不成立,
所以不能把库存的A、B、C3种零件都恰好用完.
【解析】易得库存的A,B,C的零件个数,假设生产甲x件,乙y件,丙z件恰好将3种零件都用完,等量关系为:甲的零件个数×2+丙的零件个数×2=A的零件总数;甲的零件个数×2+乙的零件个数×1=B的零件总数;乙的零件个数×1+丙的零件个数×1=C的零件总数;把所给式子整理,消去一个未知数,得到不存在的情况即可.
【考点精析】解答此题的关键在于理解解三元一次方程组的相关知识,掌握通过“代入”或“加减”消元,把“三元”化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而转化为解一元一次方程.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
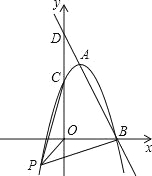
【题目】如图,已知直线y=kx+6与抛物线y=![]() +bx+c相交于A,B两点,且点A(1,4)为抛物线的顶点,点B在x轴上.
+bx+c相交于A,B两点,且点A(1,4)为抛物线的顶点,点B在x轴上.
(1)求抛物线的解析式;
(2)在(1)中抛物线的第三象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组决定去市场购买A,B,C三种仪器,其单价分别为3元,5元,7元,购买这批仪器需花62元;经过讨价还价,最后以每种单价各下降1元成交,结果只花50元就买下了这批仪器.那么A种仪器最多可买( )
A.8件
B.7件
C.6件
D.5件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2﹣2x+4化为y=a(x﹣h)2+k的形式,下列正确的是( )
A.y=(x﹣1)2+2
B.y=(x﹣1)2+3
C.y=(x﹣2)2+2
D.y=(x﹣2)2+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P1(﹣1,y1),P2(3,y2),P3(5,y3)均在二次函数y=﹣x2+2x+c的图象上,则y1 , y2 , y3的大小关系是( )
A.y3>y2>y1
B.y3>y1=y2
C.y1>y2>y3
D.y1=y2>y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 观察下列等式:31﹣1=2,32﹣1=8,33﹣1=26,34﹣1=80,35﹣1=242,….通过观察,用你所发现的规律确定32008﹣1的个位数字是___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com