
【题目】如图,已知直线y=kx+6与抛物线y=![]() +bx+c相交于A,B两点,且点A(1,4)为抛物线的顶点,点B在x轴上.
+bx+c相交于A,B两点,且点A(1,4)为抛物线的顶点,点B在x轴上.
(1)求抛物线的解析式;
(2)在(1)中抛物线的第三象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标.
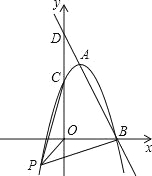
【答案】(1)y=![]() +2x+3;(2)存在;P(
+2x+3;(2)存在;P(![]() ,
,![]() );(3)(0,
);(3)(0,![]() )或(0,
)或(0,![]() )或(0,1)或(0,3).
)或(0,1)或(0,3).
【解析】
试题分析:(1)由待定系数法确定函数解析式;
(2)先确定出点C坐标,再由△POB≌△POC建立方程,求解即可,
(3)分三种情况计算,分别判断![]() ∽△DOB,
∽△DOB,![]() ∽△DOB,
∽△DOB,![]() ∽
∽![]() ,列出比例式建立方程求解即可.
,列出比例式建立方程求解即可.
试题解析:(1)把A(1,4)代入y=kx+6,
∴k=﹣2,
∴y=﹣2x+6,
由y=﹣2x+6=0,得x=3
∴B(3,0).
∵A为顶点
∴设抛物线的解析为y=![]() +4,
+4,
∴a=﹣1,
∴y=![]() +4=
+4=![]() +2x+3;
+2x+3;
(2)存在.理由如下:
当x=0时y=![]() +2x+3=3,
+2x+3=3,
∴C(0,3)
∵OB=OC=3,OP=OP,
∴当∠POB=∠POC时,△POB≌△POC,
作PM⊥x轴于M,作PN⊥y轴于N,
∴∠POM=∠PON=45°.
∴PM=PN
∴设P(m,m),则m=![]() +2m+3,
+2m+3,
∴m=![]() ,
,
∵点P在第三象限,
∴P(![]() ,
,![]() );
);
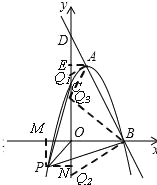
(3)①如图,当![]() =90°时,作AE⊥y轴于E,
=90°时,作AE⊥y轴于E,
∴E(0,4)
∵![]() =∠DOB=90°,
=∠DOB=90°,![]() =∠BDO,
=∠BDO,
∴![]() ∽△DOB,
∽△DOB,
∴![]() ,即
,即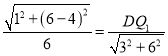 ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() (0,
(0,![]() );
);
②如图,
当![]() =90°时,∠DBO+
=90°时,∠DBO+![]() =
=![]() +
+![]() =90°,
=90°,
∴∠DBO=![]() ,
,
∵∠DOB=![]() =90°,
=90°,
∴![]() ∽△DOB,
∽△DOB,
∴![]() ,
,
∴![]() ,
,
∴![]() =
=![]() ,
,
∴![]() (0,
(0,![]() );
);
③如图,当![]() =90°时,
=90°时,![]() =
=![]() =90°,
=90°,
∴![]() =90°,
=90°,
∴
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() =0,
=0,
∴![]() =1或3,
=1或3,
∴![]() (0,1)或(0,3).
(0,1)或(0,3).
综上,Q点坐标为(0,![]() )或(0,
)或(0,![]() )或(0,1)或(0,3).
)或(0,1)或(0,3).


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=![]() +bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,
+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,![]() )、点B(
)、点B(![]() ,
,![]() )、点C(
)、点C(![]() ,
,![]() )在该函数图象上,则
)在该函数图象上,则![]() <
<![]() <
<![]() ;(5)若方程a(x+1)(x﹣5)=﹣3的两根为
;(5)若方程a(x+1)(x﹣5)=﹣3的两根为![]() 和
和![]() ,且
,且![]() <
<![]() ,则
,则![]() <﹣1<5<
<﹣1<5<![]() .其中正确的结论有( ).
.其中正确的结论有( ).

A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,且OA、OB的长满足|OA﹣8|+(OB﹣6)2=0,∠ABO的平分线交x轴于点C过点C作AB的垂线,垂足为点D,交y轴于点E.
(1)求线段AB的长;
(2)求直线CE的解析式;
(3)若M是射线BC上的一个动点,在坐标平面内是否存在点P,使以A、B、M、P为顶点的四边形是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】组装甲、乙、丙3种产品,需用A、B、C3种零件.每件甲需用A、B各2个;每件乙需用B、C各1个;每件丙需用2个A和1个C.用库存的A、B、C3种零件,如组装成p件甲产品、q件乙产品、r件丙产品,则剩下2个A和1个B,C恰好用完.求证:无论怎样改变生产甲、乙、丙的件数,也不能把库存的A、B、C3种零件都恰好用完.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com