
分析 (1)根据乘法的分配律可以解答本题;
(2)根据幂的乘方、有理数的乘法和减法可以解答本题.
解答 解:(1)$\frac{7}{22}$×(-5)+(-$\frac{7}{22}$)×9-$\frac{7}{22}$×8
=$\frac{7}{22}×[(-5)+(-9)+(-8)]$
=$\frac{7}{22}×(-22)$
=-7;
(2)-14-$\frac{1}{4}$×[2-(-4)2]
=-1-$\frac{1}{4}×[2-16]$
=-1-$\frac{1}{4}×(-14)$
=-1+$\frac{7}{2}$
=$\frac{5}{2}$.
点评 本题考查有理数的混合运算,解答此类问题的关键是明确有理数混合运算的计算方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AD,AE分别是△ABC的高和角平分线.
如图,在△ABC中,AD,AE分别是△ABC的高和角平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
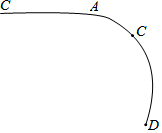 如图,一段圆弧AB上有一个点D,直线AC与圆弧相切于点A,请借助于切点A及B、D两点,利用尺规作图找出这段圆弧所在圆的圆心(不写作法,保留作图痕迹).
如图,一段圆弧AB上有一个点D,直线AC与圆弧相切于点A,请借助于切点A及B、D两点,利用尺规作图找出这段圆弧所在圆的圆心(不写作法,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com