
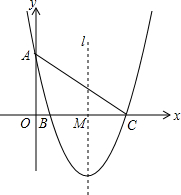
 ��ͼ����ƽ��ֱ������ϵxOy�У���֪������y=a��x-1����x-5����x�ύ��B��C���㣬��y�ύ�ڵ�A��0��4���������ߵĶԳ���l��x���ཻ�ڵ�M��
��ͼ����ƽ��ֱ������ϵxOy�У���֪������y=a��x-1����x-5����x�ύ��B��C���㣬��y�ύ�ڵ�A��0��4���������ߵĶԳ���l��x���ཻ�ڵ�M������ ��1�����Ȱ�x=0��y=4����y=a��x-1����x-5�������a��ֵ�Ƕ��٣�Ȼ�����B��C��������꣬ȷ�����������ߵĶԳ��ἴ�ɣ�
��2�����ȹ���N��NG��y�ύAC��G�����ֱ��AC�Ľ���ʽΪ��y=-$\frac{4}{5}$x+4����N��ĺ�������t�����ʱ��N��t��$\frac{4}{5}$t2-$\frac{24}{5}t$+4����0��t��5����Ȼ�������CAN��������ֵΪ���٣��жϳ��Ƿ����һ��N��ʹ��NAC�����Ϊ14���ɣ�
��3�������жϳ���A��O��M��PΪ������ı����������ߣ�AO=4��OM=3���жϳ���1��2��3��4Ϊ����2��3��4��5Ϊ�߶����������⣬���������ߵij�ֻ����3��4��5��6һ�������Ȼ��֤����A��O��M��PΪ������ı��ε������ߵij���3��4��5��6�����������P�������Ƕ��ټ��ɣ�
��� �⣺��1����x=0��y=4����y=a��x-1����x-5����
�ɵ�a����-1������-5��=4��
���a=$\frac{4}{5}$��
��B��C���������ֱ��ǣ�1��0������5��0����
��������ߵĶԳ���Ϊx=��5+1����2=3��
���������ߵĶԳ���Ϊx=3��
��2����ͼ1������N��NG��y�ύAC��G��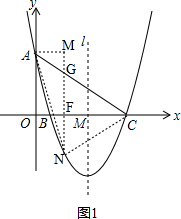 ��
��
������y=$\frac{4}{5}$��x-1����x-5��=$\frac{4}{5}$x2$-\frac{24}{5}x$+4��
�ɵ�A��0��4���͵�C��5��0�����ɵ�ֱ��AC�Ľ���ʽΪ��y=-$\frac{4}{5}$x+4��
��N��ĺ�������t�����ʱ��N��t��$\frac{4}{5}$t2-$\frac{24}{5}t$+4����0��t��5����
��x=t����y=-$\frac{4}{5}$x+4��
�ɵ�G��t��-$\frac{4}{5}$t+4����
��ʱNG=-$\frac{4}{5}$t+4-��$\frac{4}{5}$t2-$\frac{24}{5}t$+4��=-$\frac{4}{5}$t2+4t��
��S��NAC=S��ANG+S��CGN=$\frac{1}{2}��5$����-$\frac{4}{5}$t2+4t��=-2t2+10t=-2${��t-\frac{5}{2}��}^{2}$+$\frac{25}{2}$��
�൱t=$\frac{5}{2}$ʱ����NAC��������ֵΪ��$\frac{25}{2}��14$��
����ֱ��AC�·����������ϲ�����һ��N��ʹ��NAC�����Ϊ14��
��3����ͼ2��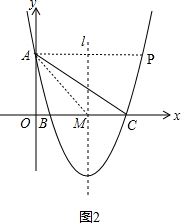 ��
��
��A��O��M��PΪ������ı����������ߣ�AO=4��OM=3��
�֡ߵ�P��������x��5��
��MP��2��AP��2��
����1��2��3��4Ϊ����2��3��4��5Ϊ�߶����������⣬
�������ߵij�ֻ����3��4��5��6һ�������
��Rt��AOM��AM=$\sqrt{{OA}^{2}{+OM}^{2}}$=5��
�������ߵĶԳ������M��
����������x��5��ͼ�����й��ڵ�A�ĶԳƵ���M�ľ���Ϊ5��
��PM=5����ʱ��P������Ϊ6����AP=6��
����A��O��M��PΪ������ı��ε������ߵij���3��4��5��6������
��P��6��4����
�ʴ�Ϊ��$\frac{4}{5}$��x=3��
���� ��1��������Ҫ�����˶��κ����ۺ��⣬�����˷������������������˷�������˼���Ӧ�ã������˴���֪����ͼ���л�ȡ��Ϣ���������û�ȡ����Ϣ�����Ӧ�������������
��2����������������ε���������Լ����ν�Ϸ�����Ӧ�ã�Ҫ�������գ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �� | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| �� | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����2��2����������������9����㣬�Ѿ�ȡ����A��B�������µ�7��������ȡһ��C��ʹ��ABC����ֱ�������εĸ�����$\frac{3}{7}$��
��ͼ����2��2����������������9����㣬�Ѿ�ȡ����A��B�������µ�7��������ȡһ��C��ʹ��ABC����ֱ�������εĸ�����$\frac{3}{7}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ѡ�� | �� | �� | �� | �� |
| �����2�� | 0.31 | 1.4 | 2.2 | 0.5 |
| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
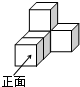 ������ͼ�������ȫ��ͬ��������ѳɵ����壬����һ���������ͼ�ǣ�������
������ͼ�������ȫ��ͬ��������ѳɵ����壬����һ���������ͼ�ǣ�������| A�� | 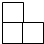 | B�� | 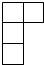 | C�� | 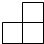 | D�� | 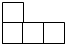 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-x��6�£�-x��2=-x4 | B�� | $\sqrt{{x}^{2}+{y}^{2}}$=x+y��x��0��y��0�� | ||
| C�� | x��y•$\frac{1}{y}$=x | D�� | 0-��-1��=1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com