
【题目】下表是二次函数y=ax2+bx+c的部分x,y的对应值:
x | … | -1 | - | 0 |
| 1 |
| 2 |
| 3 | … |
y | … | 2 |
| -1 | - | -2 | - | -1 |
| 2 | … |
(1)此二次函数图象的顶点坐标是 ;
(2)当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时,n的取值范围是 。
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:
(1)观察、分析表格中的数据可知,当x=0和x=2时,y的值都是-1,由此可确定该二次函数的图象关于直线x=1对称,而当x=1时,y=-2,由此可得抛物线的顶点坐标为(1,-2);
(2)由抛物线的顶点(1,-2)在直线y=x+n的下方可得,在y=x+n中,当x=1时,y>-2,由此可得:1+n>-2,解此不等式即可得到n的取值范围.
试题解析:
(1)观察、分析表格中的数据可知,当x=0和x=2时,y的值都是-1,
∴二次函数y=ax2+bx+c的对称轴为直线:x=1,
∵当x=1时,y=-2,
∴二次函数y=ax2+bx+c的顶点坐标为(1,-2);
(2)∵抛物线y=ax2+bx+c的顶点(1,-2)在直线y=x+n的下方,
∴在y=x+n中,当x=1时,y>-2,由此可得:1+n>-2,解得n>-3,
∴n的取值范围为:n>-3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】数轴上两点间的距离等于这两个点所对应的数的差的绝对值.例:点A、B在数轴上对应的数分别为a、b,则A、B两点间的距离表示为AB=|a﹣b|.根据以上知识解题:
(1)点A在数轴上表示3,点B在数轴上表示2,那么AB=_______.
(2)在数轴上表示数a的点与﹣2的距离是3,那么a=______.
(3)如果数轴上表示数a的点位于﹣4和2之间,那么|a+4|+|a﹣2|=______.
(4)对于任何有理数x,|x﹣3|+|x﹣6|是否有最小值?如果有,直接写出最小值.如果没有.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在普通商场中用96元购买了一种商品,后来他在网上发现完全相同的这一商品在网上购买比普通商场中每件少2元,他用90元在网上再次购买这一商品,比上次在普通商场中多买了3件.问小明在网上购买的这一商品每件几元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,点P为边BC上一动点,连接AP,将线段AP绕点P顺时针旋转90°,点A恰好落在直线CD上点E处
(1) 如图1,点E在线段CD上,求证:AD+DE=2AB
(2) 如图2,点E在线段CD的延长线上,且点D 为线段CE的中点,在线段BD上取点F,连接AF、PF,若AF=AB,求证:∠APF=∠ADB
(3) 如图3,点E在线段CD上,连接BD.若AB=2,BD∥PE,则DE=___________ (直接写出结果)
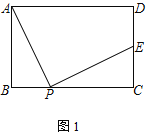
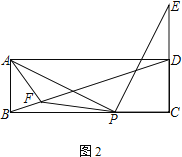
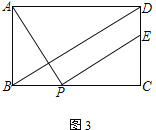
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC,∠BAC=90°,点D,E分别为边AB,BC的中点,点F在CA延长线上,且∠FDA=∠B.
(1)求证:AF=DE;
(2)若AC=3,BC=5,求四边形AEDF的周长.
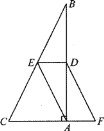
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青岛交运集团出租车司机张师傅某天下午的营运全是在东西走向的吉林路上进行的,如果规定向东为正,向西为负,他这天下午行车里程![]() 单位:千米
单位:千米![]() 如下:
如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)张师傅这天最后到达目的地时,在下午出车时的出发地哪个方向?距离出发地多远?
(2)张师傅这天下午共行车多少千米?
(3)若每千米耗油![]() ,则这天下午张师傅用了多少升油?
,则这天下午张师傅用了多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中点A的坐标为(0,6),点B的坐标为(﹣![]() ,5),将△AOB沿x轴向左平移得到△A′O′B′,点A的对应点A′落在直线y=﹣
,5),将△AOB沿x轴向左平移得到△A′O′B′,点A的对应点A′落在直线y=﹣![]() x上,则点B的对应点B′的坐标为( )
x上,则点B的对应点B′的坐标为( )
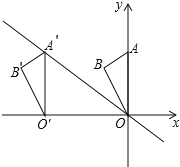
A.(﹣8,6)B.(﹣![]() ,5)C.(﹣
,5)C.(﹣![]() ,5)D.(﹣8,5)
,5)D.(﹣8,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com