
分析 (1)先求得BC的长,然后根据中点的定义求得MC和CN的长,从而可求得MN的长;
(2)(3)根据中点的定义可知:MC=$\frac{1}{2}AC$,NC=$\frac{1}{2}BC$,然后根据MN=MC+NC=$\frac{1}{2}AC+\frac{1}{2}BC=\frac{1}{2}AB$求解即可.
解答 解:(1)如图所示:
BC=AB-AC=10-4=6cm,
∵M是AC的中点,N是BC的中点,
∴MC=$\frac{1}{2}AC=\frac{1}{2}×4$=2,NC=$\frac{1}{2}CB=\frac{1}{2}×6$=3,
∴MN=MC+CN=2+3=5cm;
(2)∵M是AC的中点,N是BC的中点,
MC=$\frac{1}{2}AC$,NC=$\frac{1}{2}BC$
∴MN=MC+NC=$\frac{1}{2}AC+\frac{1}{2}BC=\frac{1}{2}AB=\frac{1}{2}a$,
(3)当点C在AB上移动时,MN的长不变.
∵M是AC的中点,N是BC的中点,
MC=$\frac{1}{2}AC$,NC=$\frac{1}{2}BC$
∴MN=MC+NC=$\frac{1}{2}AC+\frac{1}{2}BC=\frac{1}{2}AB$.
点评 本题主要考查的是线段的中点的定义,根据线段中点的定义得到:MC=$\frac{1}{2}AC$,NC=$\frac{1}{2}BC$,从而得出MN=$\frac{1}{2}AC+\frac{1}{2}BC=\frac{1}{2}AB$是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
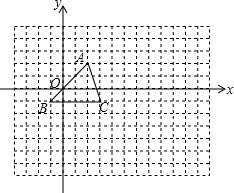 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立如图所示的平面直角坐标系后,△ABC的顶点均在格点上,且坐标分别为:A(2,2),B(-1,-1),C(3,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立如图所示的平面直角坐标系后,△ABC的顶点均在格点上,且坐标分别为:A(2,2),B(-1,-1),C(3,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 筐 数 | 2 | 5 | 3 | 4 | 2 | 4 |
| 与标准重量比较(千克) | -0.8 | +0.6 | -0.5 | -0.4 | +0.5 | -0.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次课堂调研数学试卷(解析版) 题型:解答题
如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。
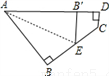
(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com