
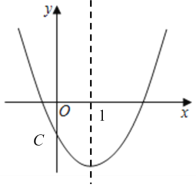
【题目】如图,若b是正数,直线l:y=b与y轴交于点A;直线a:y=x﹣b与y轴交于点B;抛物线L:y=﹣x2+bx的顶点为C,且L与x轴右交点为D.
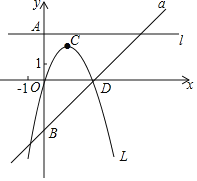
(1)若AB=8,求b的值,并求此时L的对称轴与a的交点坐标;
(2)当点C在l下方时,求点C与l距离的最大值;
(3)设x0≠0,点(x0,y1),(x0,y2),(x0,y3)分别在l,a和L上,且y3是y1,y2的平均数,求点(x0,0)与点D间的距离;
(4)在L和a所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出b=2019和b=2019.5时“美点”的个数.
【答案】(1)b=4,(2,﹣2 );(2)1;(3)![]() ;(4)当b=2019时“美点”的个数为4040个,b=2019.5时“美点”的个数为1010个.
;(4)当b=2019时“美点”的个数为4040个,b=2019.5时“美点”的个数为1010个.
【解析】
(1)求出A、B 的坐标,由AB=8,可求出b的值.从而得到L的解析式,找出L的对称轴与a的交点即可;
(2)通过配方,求出L的顶点坐标,由于点C在l下方,则C与l的距离![]() ,配方即可得出结论;
,配方即可得出结论;
(3)由題意得y1+y2=2y3,进而有b+x0﹣b=2(﹣x02+bx0)解得x0的值,求出L与x轴右交点为D的坐标,即可得出结论;
(4)①当b=2019时,抛物线解析式L:y=﹣x2+2019x直线解析式a:y=x﹣2019,美点”总计4040个点,②当b=2019.5时,抛物线解析式L:y=﹣x2+2019.5x,直线解析式a:y=x﹣2019.5,“美点”共有1010个.
(1)当x=0吋,y=x﹣b=﹣b,∴B (0,﹣b).
∵AB=8,而A(0,b),∴b﹣(﹣b)=8,∴b=4,∴L:y=﹣x2+4x,∴L的对称轴x=2,当x=2时,y=x﹣4=﹣2,∴L的对称轴与a的交点为(2,﹣2 );
(2)y=﹣(x![]() )2
)2![]() ,∴L的顶点C(
,∴L的顶点C(![]() ,
,![]() ).
).
∵点C在l下方,∴C与l的距离b![]() (b﹣2)2+1≤1,∴点C与l距离的最大值为1;
(b﹣2)2+1≤1,∴点C与l距离的最大值为1;
(3)∵y3是y1,y2的平均数,∴y1+y2=2y3,∴b+x0﹣b=2(﹣x02+bx0),解得:x0=0或x0=b![]() .
.
∵x0≠0,∴x0=b![]() ,对于L,当y=0吋,0=﹣x2+bx,即0=﹣x(x﹣b),解得:x1=0,x2=b.
,对于L,当y=0吋,0=﹣x2+bx,即0=﹣x(x﹣b),解得:x1=0,x2=b.
∵b>0,∴右交点D(b,0),∴点(x0,0)与点D间的距离b﹣(b![]() )
)![]() .
.
(4)①当b=2019时,抛物线解析式L:y=﹣x2+2019x,直线解析式a:y=x﹣2019.
联立上述两个解析式可得:x1=﹣1,x2=2019,∴可知每一个整数x的值都对应的一个整数y值,且﹣1和2019之间(包括﹣1和﹣2019)共有2021个整数;
∵另外要知道所围成的封闭图形边界分两部分:线段和抛物线,∴线段和抛物线上各有2021个整数点,∴总计4042个点.
∵这两段图象交点有2个点重复,∴美点”的个数:4042﹣2=4040(个);
②当b=2019.5时,抛物线解析式L:y=﹣x2+2019.5x,直线解析式a:y=x﹣2019.5,联立上述两个解析式可得:x1=﹣1,x2=2019.5,∴当x取整数时,在一次函数y=x﹣2019.5上,y取不到整数值,因此在该图象上“美点”为0,在二次函数y=x2+2019.5x图象上,当x为偶数时,函数值y可取整数,可知﹣1到2019.5之 间有1010个偶数,因此“美点”共有1010个.
故b=2019时“美点”的个数为4040个,b=2019.5时“美点”的个数为1010个.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】某数学社团成员想利用所学的知识测量某广告牌的宽度![]() 图中线段MN的长
图中线段MN的长![]() ,直线MN垂直于地面,垂足为点
,直线MN垂直于地面,垂足为点![]() 在地面A处测得点M的仰角为
在地面A处测得点M的仰角为![]() 、点N的仰角为
、点N的仰角为![]() ,在B处测得点M的仰角为
,在B处测得点M的仰角为![]() ,
,![]() 米,且A、B、P三点在一直线上
米,且A、B、P三点在一直线上![]() 请根据以上数据求广告牌的宽MN的长.
请根据以上数据求广告牌的宽MN的长.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了预防流行性感冒,对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量![]() 与时间
与时间![]() 成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物6min燃毕,此时室内空气中每立方米的含药量为4mg,
成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物6min燃毕,此时室内空气中每立方米的含药量为4mg,
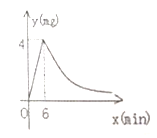
(1)写出药物燃烧前后,y与x之间的函数表达式;
(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过多少分钟,学生方能回到教室?
(3)研究表明,当空气中每立方米的含药量不低于2mg且持续时间不低于9min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?
查看答案和解析>>
科目:初中数学 来源: 题型:
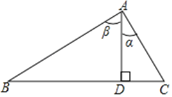
【题目】如图,在Rt△ABC中,∠A=90°,AD⊥BC,垂足为D.给出下列四个结论:①sinα=sinB;②sinα=cosβ;③![]() ;④
;④![]() .其中正确的结论有____________.
.其中正确的结论有____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示则下列结论:①4a﹣b=0;②c<0;③c>3a;④4a﹣2b>at2+bt(t为实数);⑤点(﹣![]() ,y1),(﹣
,y1),(﹣![]() ,y2),(
,y2),(![]() )是该抛物线上的点,则y2<y1<y3,其中,正确结论的个数是( )
)是该抛物线上的点,则y2<y1<y3,其中,正确结论的个数是( )
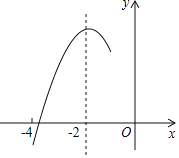
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义: 在平面直角坐标系中,如果点![]() 和
和![]() 都在某函数的图象
都在某函数的图象![]() 上,则称点
上,则称点![]() 是图象
是图象![]() 的一对“相关点”.例如,点
的一对“相关点”.例如,点![]() 和点
和点![]() 是直线
是直线![]() 的一对相关点.
的一对相关点.
![]() 请写出反比例函数
请写出反比例函数![]() 的图象上的一对相关点的坐标;
的图象上的一对相关点的坐标;
![]() 如图,抛物线
如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 求抛物线的解析式:
求抛物线的解析式:
![]() 若点
若点![]() 是抛物线
是抛物线![]() 上的一对相关点,直线
上的一对相关点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为抛物线
为抛物线![]() 上之间的一点,求
上之间的一点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
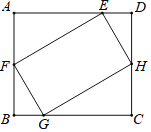
【题目】如图,矩形EFGH的四个顶点分别在矩形ABCD的各条边上,AB=EF,FG=2,GC=3.有以下四个结论:①∠BGF=∠CHG;②△BFG≌△DHE;③tan∠BFG=![]() ;④矩形EFGH的面积是4
;④矩形EFGH的面积是4![]() .其中一定成立的是______.(把所有正确结论的序号填在横线上)
.其中一定成立的是______.(把所有正确结论的序号填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中AD∥BC,∠A=90°,AB=6,BC=10,点E为边AD上一点,将ABE沿BE翻折,点A落在对角线BD上的点G处,连接EG并延长交射线BC于点F.
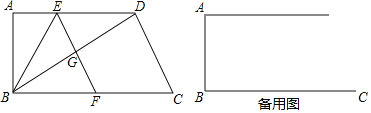
(1)如果cos∠DBC![]() ,求EF的长;
,求EF的长;
(2)当点F在边BC上时,连接AG,设AD=x,![]() y,求y关于x的函数关系式并写出x的取值范围;
y,求y关于x的函数关系式并写出x的取值范围;
(3)连接CG,如果△FCG是等腰三角形,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
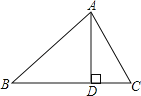
【题目】如图,在△ABC中,AD⊥BC于D,下列条件:(1)∠B+∠DAC=90°;(2)∠B=∠DAC;(3)![]() ;(4)AB2=BDBC.其中一定能够判定△ABC是直角三角形的有(填序号)_____.
;(4)AB2=BDBC.其中一定能够判定△ABC是直角三角形的有(填序号)_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com