
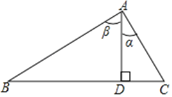
【题目】如图,在Rt△ABC中,∠A=90°,AD⊥BC,垂足为D.给出下列四个结论:①sinα=sinB;②sinα=cosβ;③![]() ;④
;④![]() .其中正确的结论有____________.
.其中正确的结论有____________.
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是AC、BC为直径作半圆弧的中点,![]() ,
,![]() 的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
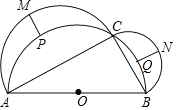
A.17B.18C.19D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数 y=kx+b 的图像如图所示,则当kx+b>0 时,x 的取值范围为___________.

【答案】x>1
【解析】分析:题目要求 kx+b>0,即一次函数的图像在x 轴上方时,观察图象即可得x的取值范围.
详解:
∵kx+b>0,
∴一次函数的图像在x 轴上方时,
∴x的取值范围为:x>1.
故答案为:x>1.
点睛:本题考查了一次函数与一元一次不等式的关系,主要考查学生的观察视图能力.
【题型】填空题
【结束】
16
【题目】菱形ABCD中, ![]() ,其周长为32,则菱形面积为____________.
,其周长为32,则菱形面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,且过点(﹣3,0),(1,0),下列说法错误的是( )

A.2a﹣b=0
B.4a﹣2b+c<0
C.(﹣4,y1),(2,y2)是抛物线上两点,则y1>y2
D.y<0时,﹣3<x<1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
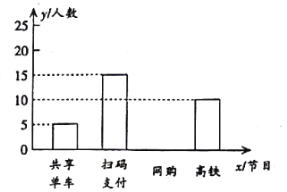
【题目】为了了解某小区青年对“高铁”、“扫码支付”、“网购”和“共享单车”新四大发明的喜爱程度,随机调查该小区一部分青年(每名青年只能选一个),并将调查结果制成如图所示统计表与条形统计图.
青年最喜爱的新四大发明人数统计表
节目 | 人数(名) | 百分比 |
共享单车 | 5 |
|
扫码支付 | 15 |
|
网购 |
|
|
高铁 | 10 |
|
青年最喜爱的新四大发明人数条形统计图
(1)计算![]() 的值
的值![]() ;
;
(2)请补全条形统计图;
(3)在被调查喜爱“共享单车”青年中,小明一周内使用共享单车的次数分别为:1,3,5,12,![]() ,若整数
,若整数![]() 是这组数据的中位数,直接写出该组数据的平均数.
是这组数据的中位数,直接写出该组数据的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若b是正数,直线l:y=b与y轴交于点A;直线a:y=x﹣b与y轴交于点B;抛物线L:y=﹣x2+bx的顶点为C,且L与x轴右交点为D.
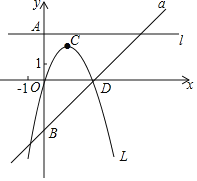
(1)若AB=8,求b的值,并求此时L的对称轴与a的交点坐标;
(2)当点C在l下方时,求点C与l距离的最大值;
(3)设x0≠0,点(x0,y1),(x0,y2),(x0,y3)分别在l,a和L上,且y3是y1,y2的平均数,求点(x0,0)与点D间的距离;
(4)在L和a所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出b=2019和b=2019.5时“美点”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.
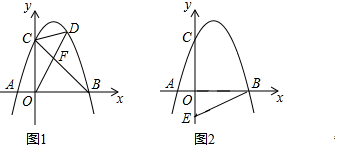
(1)求该抛物线的函数解析式;
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD,OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
(3)如图2,点E的坐标为(0,![]() ),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据爱因斯坦的相对论可知,任何物体的运动速度不能超过光速(3×105km/s),因为一个物体达到光速需要无穷多的能量,并且时光会倒流,这在现实中是不可能的.但我们可让一个虚拟物超光速运动,例如:直线l,m表示两条木棒相交成的锐角的度数为10°,它们分别以与自身垂直的方向向两侧平移时,它们的交点A也随着移动(如图箭头所示),如果两条直线的移动速度都是光速的0.2倍,则交点A的移动速度是光速的_____倍.(结果保留两个有效数字).
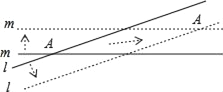
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com