
分析 (1)根据接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,直接得出生产这批空调的时间为x天,与每天生产的空调为y台之间的函数关系式;
(2)根据基本等量关系:利润=(每台空调订购价-每台空调成本价-增加的其他费用)×生产量即可得出答案.
解答 解:(1)∵接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,
∴由题意可得出,第x天生产空调y台,y与x之间的函数解析式为:y=40+2x(1≤x≤10);
(2)当1≤x≤5时,W=(2920-2000)×(40+2x)=1840x+36800,
∵1840>0,
∴W随x的增大而增大,
∴当x=5时,W最大值=1840×5+36800=46000;
当5<x≤10时,
W=[2920-2000-20(40+2x-50)]×(40+2x)=-80(x-4)2+46080,
此时函数图象开口向下,在对称轴右侧,W随着x的增大而减小,又天数x为整数,
∴当x=6时,W最大值=45760元.
∵46000>45760,
∴当x=5时,W最大,且W最大值=46000元.
综上所述:W=$\left\{\begin{array}{l}{1840x+36800(1≤x≤5)}\\{-80(x-4)^{2}+46080(5<x≤10)}\end{array}\right.$.
点评 此题主要考查了二次函数的应用以及分段函数,如何分段,怎样表达每个分段函数,并比较确定最大值是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | b2=c2-a2 | B. | a:b:c=3:4:5 | C. | ∠C=∠A-∠B | D. | ∠A:∠B:∠C=3:4:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
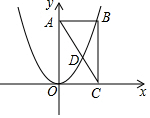 如图,抛物线y=ax2经过矩形OABC的顶点B,交对角线AC于点D.则$\frac{AD}{AC}$的值为$\frac{\sqrt{5}-1}{2}$.
如图,抛物线y=ax2经过矩形OABC的顶点B,交对角线AC于点D.则$\frac{AD}{AC}$的值为$\frac{\sqrt{5}-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1=y2 | B. | y1>y2 | C. | y1<y2 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com