
【题目】如图,![]() 于点
于点![]() ,
,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,当
,当![]() 绕点
绕点![]() 旋转时,记
旋转时,记![]() .
.
(1)过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,作射线
,作射线![]() 交射线
交射线![]() 于点
于点![]() .
.
①依题意补全图形,求![]() 的度数;
的度数;
②当![]() 时,求
时,求![]() 的长.
的长.
(2)若![]() 上存在一点
上存在一点![]() ,且
,且![]() ,作射线
,作射线![]() 交射线
交射线![]() 于点
于点![]() ,直接写出
,直接写出![]() 长度的最大值.
长度的最大值.
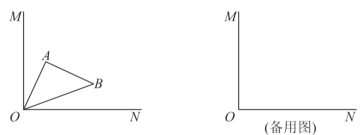
【答案】(1)①见解析, 45°②7;(2)见解析,![]()
【解析】
(1)①作![]() 于点H,
于点H,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,证明AHO≌AGB, 即可求得∠ODC的度数;
,证明AHO≌AGB, 即可求得∠ODC的度数;
②延长![]() 交
交![]() 于点
于点![]() ,利用条件可求得AK、OK的长度,于是可求OD的长;
,利用条件可求得AK、OK的长度,于是可求OD的长;
(2)分析可知,点B在以O为圆心,OB为半径的圆上运动(![]() 个圆),所以当PB是圆O的切线时,PQ的值最大,据此可解.
个圆),所以当PB是圆O的切线时,PQ的值最大,据此可解.
解:(1)①补全图形如图所示,过点![]() 作
作![]() 于点H,
于点H,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
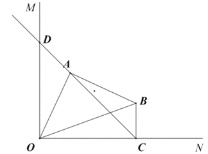

∵![]() ,
,![]() ,
,![]() ,
,
∴∠AGB=∠AHO=∠C =![]() ,
,
∴∠GAH=![]() ,
,
∴∠OAH+∠HAB=∠GAB+∠HAB=![]() ,
,
∴∠OAH =∠GAB, 四边形![]() 为矩形,
为矩形,
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴OA=AB,
∴AHO≌AGB,
∴AH=AG,
∴四边形![]() 为正方形,
为正方形,
∴∠OCD=45°,
∴∠ODC=45°;
②延长![]() 交
交![]() 于点
于点![]() ,
,

∵![]() ,OA=5,
,OA=5,
∴AK=4,
∴OK=3,
∵∠ODC=45°,
∴DK=AK=4
∴![]() ;
;
(2)如图,

∵![]() 绕点
绕点![]() 旋转,
旋转,![]()
∴点B在以O为圆心,OB为半径的圆上运动(![]() 个圆),
个圆),
∴当PB是圆O的切线时,PQ的值最大,
∵![]()
∴![]()
∴∠OPB=45°,
∴ OQ=OP=10,
∴![]() .
.
∴![]() 长度的最大值是
长度的最大值是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,聪聪想在自己家的窗口A处测量对面建筑物CD的高度,他首先量出窗口A到地面的距离(AB)为16m,又测得从A处看建筑物底部C的俯角α为30°,看建筑物顶部D的仰角β为53°,且AB,CD都与地面垂直,点A,B,C,D在同一平面内.

(1)求AB与CD之间的距离(结果保留根号).
(2)求建筑物CD的高度(结果精确到1m).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.
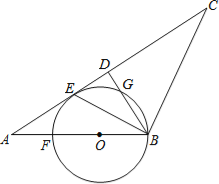
(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)当BD=6,AB=10时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6![]() ,BC=3
,BC=3![]() 动点P从点A出发,沿AC以每秒4个单位长度的速度向终点C运动.过点P(不与点A、C重合)作EF⊥AC,交AB或BC于点E,交AD或DC于点F,以EF为边向右作正方形EFGH设点P的运动时间为t秒.
动点P从点A出发,沿AC以每秒4个单位长度的速度向终点C运动.过点P(不与点A、C重合)作EF⊥AC,交AB或BC于点E,交AD或DC于点F,以EF为边向右作正方形EFGH设点P的运动时间为t秒.
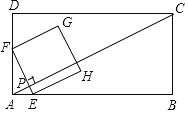
(1)①AC= .②当点F在AD上时,用含t的代数式直接表示线段PF的长 .
(2)当点F与点D重合时,求t的值.
(3)设方形EFGH的周长为l,求l与t之间的函数关系式.
(4)直接写出对角线AC所在的直线将正方形EFGH分成两部分图形的面积比为1:2时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt![]() 中,∠A=90°,AC=4,
中,∠A=90°,AC=4,![]() ,将
,将![]() 沿着斜边BC翻折,点A落在点
沿着斜边BC翻折,点A落在点![]() 处,点D、E分别为边AC、BC的中点,联结DE并延长交
处,点D、E分别为边AC、BC的中点,联结DE并延长交![]() 所在直线于点F,联结
所在直线于点F,联结![]() ,如果
,如果![]() 为直角三角形时,那么
为直角三角形时,那么![]() ____________
____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,联结PC,在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°.
(1)如图,当点P在边AB上时,如果BP=3,求线段PC的长;
(2)当点P在射线BA上时,设![]() ,求y关于
,求y关于![]() 的函数解析式及定义域;
的函数解析式及定义域;
(3)联结PQ,直线PQ与直线BC交于点E,如果![]() 与
与![]() 相似,求线段BP的长.
相似,求线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年9月8日,重庆首家海底捞在来福士广场正式开始试营业,由于重庆人偏好麻辣口味,海底捞来福士店在原有番茄、红汤牛油、菌菇等多种常规锅底的基础上,专门为重庆人私人订制了一种“双椒锅底”.开业当天,人气爆满,番茄锅和双椒锅成为最受欢迎的两种锅底,总计销售300份,销售总额为9800元.其中双椒锅的销售单价是42元,番茄锅的销售单价为28元.
(1)求开业当天番茄锅销售数量;
(2)试营业一段时间后,商家发现番茄锅和双椒锅的日均销量之比为3:2.为了庆祝国庆,回馈广大顾客,海底捞在国庆期间推出了优惠活动,在原有售价的基础上将番茄锅降价![]() a%,双椒锅降价a%进行销售.10月1日当天,番茄锅的销量比日均销量增加了a%,而双椒锅的销量比日均销量增加了2a%,结果当天这两种锅底的销售总额比日均销售总额多了
a%,双椒锅降价a%进行销售.10月1日当天,番茄锅的销量比日均销量增加了a%,而双椒锅的销量比日均销量增加了2a%,结果当天这两种锅底的销售总额比日均销售总额多了![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)求C、D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD=![]() S△BCD,求点P的坐标.
S△BCD,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com