
【题目】如图,在平面直角坐标系![]() 中,以点
中,以点![]() 为圆心画圆,与
为圆心画圆,与![]() 轴交于
轴交于![]() ;两点,与
;两点,与![]() 轴交于
轴交于![]() 两点,当
两点,当![]() 时,
时,![]() 的取值范围是____________.
的取值范围是____________.
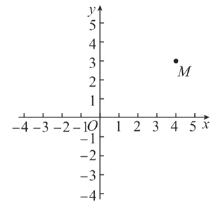
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+c(a≠0)经过C(2,0),D(0,﹣1)两点,并与直线y=kx交于A、B两点,直线l过点E(0,﹣2)且平行于x轴,过A、B两点分别作直线l的垂线,垂足分别为点M、N.

(1)求此抛物线的解析式;
(2)求证:AO=AM;
(3)探究:
①当k=0时,直线y=kx与x轴重合,求出此时![]() 的值;
的值;
②试说明无论k取何值,![]() 的值都等于同一个常数.
的值都等于同一个常数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤![]() .其中正确结论的是( )
.其中正确结论的是( )
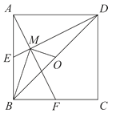
A. ①③④B. ②④⑤C. ①③⑤D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() 与点
与点![]() ,若在线段
,若在线段![]() 上存在点
上存在点![]() ,满足
,满足![]() ,则称点
,则称点![]() 为线段
为线段![]() 的“限距点”.
的“限距点”.

(1)如图,在平面直角坐标系![]() 中,若点
中,若点![]() .
.
①在![]() 中,是线段
中,是线段![]() 的“限距点”的是 ;
的“限距点”的是 ;
②点![]() 是直线
是直线![]() 上一点,若点
上一点,若点![]() 是线段
是线段![]() 的“限距点”,请求出点
的“限距点”,请求出点![]() 横坐标
横坐标![]() 的取值范围.
的取值范围.
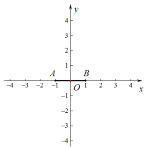
(2)在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
. ![]() 上存在线段
上存在线段![]() 的“限距点”,请求出
的“限距点”,请求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
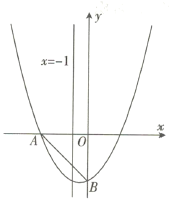
【题目】如图,抛物线![]() 与
与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,点
,点![]() 分别是直线
分别是直线![]() 与抛物线上的点,若点
与抛物线上的点,若点![]() 围成的四边形是平行四边形,则点
围成的四边形是平行四边形,则点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
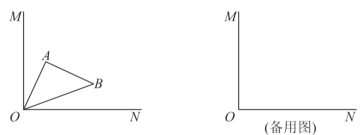
【题目】如图,![]() 于点
于点![]() ,
,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,当
,当![]() 绕点
绕点![]() 旋转时,记
旋转时,记![]() .
.
(1)过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,作射线
,作射线![]() 交射线
交射线![]() 于点
于点![]() .
.
①依题意补全图形,求![]() 的度数;
的度数;
②当![]() 时,求
时,求![]() 的长.
的长.
(2)若![]() 上存在一点
上存在一点![]() ,且
,且![]() ,作射线
,作射线![]() 交射线
交射线![]() 于点
于点![]() ,直接写出
,直接写出![]() 长度的最大值.
长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
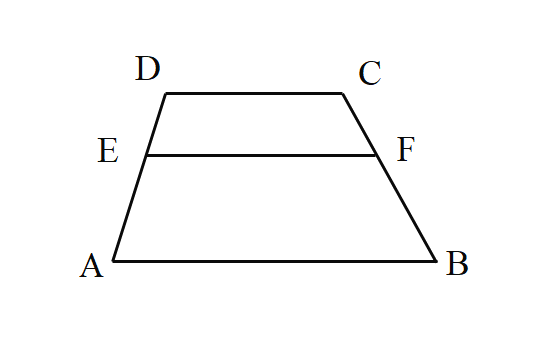
【题目】如图,已知在梯形ABCD中,AB//CD,AB=12,CD=7,点E在边AD上,![]() ,过点E作EF//AB交边BC于点F.
,过点E作EF//AB交边BC于点F.
(1)求线段EF的长;
(2)设![]() ,
,![]() ,联结AF,请用向量
,联结AF,请用向量![]() 表示向量
表示向量![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
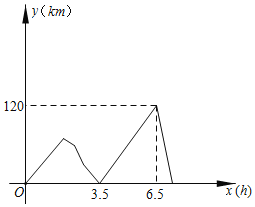
【题目】在一条笔直的公路上有A、B两地,甲、乙两车均从A地匀速驶向B地,甲车比乙车早出发2小时,出发后,甲车出现了故障停下来维修,半小时后继续以原速向B地行驶.当乙车到达B地后立刻提速50%返回,在返回途中第二次与甲车相遇.下图表示甲乙两车之间的距离y(千米)与甲车行驶的时间x(小时)之间的函数关系.则当乙车第二次与甲车相遇时,甲车距离B地_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
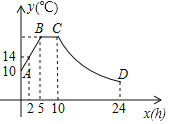
【题目】冬天即将到来,龙泉某中学的初三学生到某蔬菜生产基地作数学实验.在气温较低时,蔬菜生产基地用装有恒温系统的大棚栽培蔬菜,经收集数据,该班同学将大棚内温度和时间的关系拟合为一个分段函数,如图是某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系,其中线段AB,BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)若大棚栽种某种蔬菜,温度低于10℃时会受到伤害.问若栽种这种蔬菜,恒温系统最多可以关闭多少小时就必须再次启动,才能使蔬菜避免受到伤害?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com