
����Ŀ����ͼ��������y=ax2+c��a��0������C��2��0����D��0����1�����㣬����ֱ��y=kx����A��B���㣬ֱ��l����E��0����2����ƽ����x�ᣬ��A��B����ֱ���ֱ��l�Ĵ��ߣ�����ֱ�Ϊ��M��N��

��1����������ߵĽ���ʽ��
��2����֤��AO=AM��
��3��̽����
����k=0ʱ��ֱ��y=kx��x���غϣ������ʱ![]() ��ֵ��
��ֵ��
����˵������kȡ��ֵ��![]() ��ֵ������ͬһ��������
��ֵ������ͬһ��������
���𰸡��⣺��1��y=![]() x2��1
x2��1
��2���������
��3���������
��������
��1���ѵ�C��D��������������߽���ʽ���a��c�����ɵý⡣
��2�����������߽���ʽ�����A�����꣬Ȼ�����AO��AM�ij������ɵ�֤��
��3����k=0ʱ�����AM��BN�ij���Ȼ�����![]() ���㼴�ɵý⣻
���㼴�ɵý⣻
�����A��x1��![]() x12��1����B��x2��
x12��1����B��x2��![]() x22��1����Ȼ���ʾ��
x22��1����Ȼ���ʾ��![]() ����������������ֱ�߽���ʽ������δ֪��y�õ�����x��һԪ���η��̣����ø���ϵ���Ĺ�ϵ��ʾ��x1+x2��x12�������x12+x22��x12x22��Ȼ�������м��㼴�ɵý⡣
����������������ֱ�߽���ʽ������δ֪��y�õ�����x��һԪ���η��̣����ø���ϵ���Ĺ�ϵ��ʾ��x1+x2��x12�������x12+x22��x12x22��Ȼ�������м��㼴�ɵý⡣
�⣺��1����������y=ax2+c��a��0������C��2��0����D��0����1����
��![]() �����
�����![]() ��
��
�������ߵĽ���ʽΪy=![]() x2��1��
x2��1��
��2��֤�������A������Ϊ��m��![]() m2��1����
m2��1����
��![]() ��
��
��ֱ��l����E��0����2����ƽ����x�ᣬ����M��������Ϊ��2��
��AM=![]() m2��1������2��=
m2��1������2��=![]() m2+1��
m2+1��
��AO=AM��
��3����k=0ʱ��ֱ��y=kx��x���غϣ���A��B��x���ϣ�
��AM=BN=0������2��=2��
��![]() ��
��
��kȡ�κ�ֵʱ�����A��x1��![]() x12��1����B��x2��
x12��1����B��x2��![]() x22��1����
x22��1����
��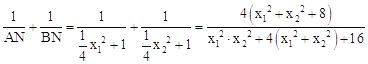 ��
��
����������y�ã�x2��4kx��4=0��
�ɸ���ϵ���Ĺ�ϵ�ã�x1+x2=4k��x1x2=��4��
��x12+x22=��x1+x2��2��2x1x2=16k2+8��x12x22=16��
��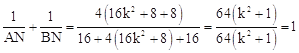 ��
��
������kȡ��ֵ��![]() ��ֵ������ͬһ������1��
��ֵ������ͬһ������1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ͳ���Ͷ��15000Ԫ�ʽ�![]() ��
��![]() ����Ʒ�ƵĿ�Ȫˮ��600�䣬��Ȫˮ�ijɱ��ۺ����ۼ����±���ʾ��
����Ʒ�ƵĿ�Ȫˮ��600�䣬��Ȫˮ�ijɱ��ۺ����ۼ����±���ʾ��
���/���� | �ɱ��ۣ�Ԫ/�䣩 | ���ۼۣ�Ԫ/�䣩 |
AƷ�� | 20 | 32 |
BƷ�� | 35 | 50 |
��1���ô��ͳ��й���![]() ��
��![]() Ʒ�ƿ�Ȫˮ�������䣿
Ʒ�ƿ�Ȫˮ�������䣿
��2��ȫ��������600���Ȫˮ���ó��й���ö�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijˮ����ֳ��ȥ����������Ϻ������ʹÿǧ��С��Ϻ��ֳ�ɱ���Ϊ6Ԫ������������������80������۵���P��Ԫ/ǧ�ˣ���ʱ���t���죩֮��ĺ�����ϵΪ��P= ����������y��ǧ�ˣ���ʱ���t���죩֮��ĺ�����ϵ��ͼ��ʾ��
����������y��ǧ�ˣ���ʱ���t���죩֮��ĺ�����ϵ��ͼ��ʾ��
��1����������y��ʱ��t�ĺ�����ϵʽ��
��2��������������ΪW��Ԫ������W��t֮��ĺ�������ʽ��
��3������������W��һ�������������Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �Ľ�ƽ�����ཻ�ڵ�
�Ľ�ƽ�����ཻ�ڵ�![]() ��
��![]() ��
Ϊ��![]() ���е㣬
���е㣬![]() ����
����![]() �� ��
�� ��

A.125��B.145��C.175��D.190��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �Ե�
�Ե�![]() ΪԲ�ģ������ⳤΪ�뾶�����ֱ�
ΪԲ�ģ������ⳤΪ�뾶�����ֱ�![]() ��
��![]() ��
��![]() ���㣬�ٷֱ��Ե�
���㣬�ٷֱ��Ե�![]() ΪԲ�ģ��Դ���
ΪԲ�ģ��Դ���![]() �ij�Ϊ�뾶�������ڵ�
�ij�Ϊ�뾶�������ڵ�![]() ��������
��������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �������
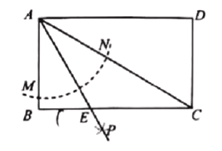
�������![]() ���������__________��
���������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��![]() �������ж��д�����ǣ� ��
�������ж��д�����ǣ� ��
A.���![]() ��
��![]() ����ô�ı���ABCD��ƽ���ı���
����ô�ı���ABCD��ƽ���ı���
B.���![]() ��
��![]() ����ô�ı���ABCD�Ǿ���
����ô�ı���ABCD�Ǿ���
C.���![]() ��
��![]() ����ô�ı���ABCD������
����ô�ı���ABCD������
D.���![]() ��AC��ֱƽ��BD����ô�ı���ABCD��������
��AC��ֱƽ��BD����ô�ı���ABCD��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ݵ��飬������ʻ��������ͨ�¹ʵ���Ҫԭ��֮һ�����Թ涨�����龳�е��ٶȲ��ó���15m/s��һ����ֱ��·BD���Ϸ�A����һ̽���ǣ���ƽ�漸��ͼ��AD=24m����D=90������һ��̽�һ���γ���B��������D����ʻ����á�ABD=31����2���C�㣬��á�ACD=50����tan31���0.6��tan50���1.2�������ȷ��1m��.
��1����B��C�ľ���.
��2��ͨ�����㣬�жϴ˽γ��Ƿ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ĩ��С����С��������ѧ����ѧ֪ʶ��������ǰС�ӵĿ�������ʱ������ѡ���˺Ӷ��ߵ�һ�ô���������ײ���Ϊ��A�����������ڵİ���ѡ���˵�B��ʹ��AB��Ӱ���ֱ������B��������BC������AB���ӳ�����ѡ���D������DE��ʹ�õ�E���C��A���ߣ�
��֪��CB��AD��ED��AD�����BC��1m��DE��1.5m��BD��8.5m������ʾ��ͼ��ͼ��ʾ���������ز�����Ϣ����ӿ�AB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס����������̶ӷֱ�ͬʱ�������κ��������ں����ij���y(m)���ھ�ʱ��x(h)֮��Ĺ�ϵ��ͼ��ʾ�������ͼ�����ṩ����Ϣ�����������:

(1)�Ҷӿ��ڵ�30mʱ������_____ h. ����6hʱ�ӱ��ҶӶ�����____ m;
(2)�������:
�ټ���![]() ��ʱ���ڣ�y��x֮��ĺ�����ϵʽ��
��ʱ���ڣ�y��x֮��ĺ�����ϵʽ��
���Ҷ���![]() ��ʱ���ڣ�y��x֮��ĺ�����ϵʽ��
��ʱ���ڣ�y��x֮��ĺ�����ϵʽ��
(3)��x Ϊ��ֵʱ���ס� �������� ʩ�����������ں����ij������?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com