
【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:

(1)乙队开挖到30m时,用了_____ h. 开挖6h时甲队比乙队多挖了____ m;
(2)请你求出:
①甲队在![]() 的时段内,y与x之间的函数关系式;
的时段内,y与x之间的函数关系式;
②乙队在![]() 的时段内,y与x之间的函数关系式;
的时段内,y与x之间的函数关系式;
(3)当x 为何值时,甲、 乙两队在 施工过程中所挖河渠的长度相等?
【答案】(1)2,10;(2)①y=10x,②y=5x+20;(3)x为4h时,甲、乙两队所挖的河渠长度相等.
【解析】
(1)此题只要认真读图,可从中找到甲、乙两队各组数据;
(2)根据图中的信息利用待定系数法即可确定函数关系式;
(3)利用(2)中的函数关系式可以解决问题.
解:(1)依题意得乙队开挖到30m时,用了2h,
开挖6h时甲队比乙队多挖了60-50=10m;
(2)①设甲队在0≤x≤6的时段内y与x之间的函数关系式y=k1x,
由图可知,函数图象过点(6,60),
∴6k1=60,
解得k1=10,
∴y=10x,
②设乙队在2≤x≤6的时段内y与x之间的函数关系式为y=k2x+b,
由图可知,函数图象过点(2,30)、(6,50),
∴ ,
,
解得![]() ,
,
∴y=5x+20;
(3)由题意,得10x=5x+20,
解得x=4(h).
∴当x为4h时,甲、乙两队所挖的河渠长度相等.
故答案为:(1)2,10;(2)①y=10x,②y=5x+20;(3)x为4h时,甲、乙两队所挖的河渠长度相等.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+c(a≠0)经过C(2,0),D(0,﹣1)两点,并与直线y=kx交于A、B两点,直线l过点E(0,﹣2)且平行于x轴,过A、B两点分别作直线l的垂线,垂足分别为点M、N.

(1)求此抛物线的解析式;
(2)求证:AO=AM;
(3)探究:
①当k=0时,直线y=kx与x轴重合,求出此时![]() 的值;
的值;
②试说明无论k取何值,![]() 的值都等于同一个常数.
的值都等于同一个常数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D,E分别在AB,BC上,∠EAD=∠EDA,点F为DE的延长线与AC的延长线的交点.
(1)求证:DE=EF;
(2)判断BD和CF的数量关系,并说明理由;
(3)若AB=3,AE=![]() ,求BD的长.
,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
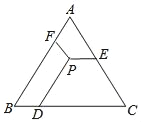
【题目】 如图,△ABC是等边三角形,P是三角形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )
A. 18B. 9![]()
C. 6D. 条件不够,不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有一个△ABC,顶点![]() ,
,![]() ,
,![]() .
.

(1)画出△ABC 关于 y 轴的对称图形![]() (不写画法)
(不写画法)
点A 关于 x 轴对称的点坐标为_____________;
点 B 关于 y 轴对称的点坐标为_____________;
点 C 关于原点对称的点坐标为_____________;
(2)若网格上的每个小正方形的边长为 1,求△ABC 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在弹性限度内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如下表,下列说法不正确的是( )
x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
y/cm | 20 | 20.5 | 21 | 21.5 | 22 | 22.5 |
A. x与y都是变量,且x是自变量,y是x的函数
B. 弹簧不挂重物时的长度为0 cm
C. 物体质量每增加1 kg,弹簧长度y增加0.5 cm
D. 所挂物体质量为7 kg时,弹簧长度为23.5 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们新定义一种三角形:两边平方和等于第三边平方的两倍的三角形叫做奇异三角形.
(1)根据“奇异三角形”的定义,请你判断命题“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,点C是⊙O上一点(不与点A,B重合),D是半圆![]() 的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
求证:△ACE是奇异三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球2个,蓝球1个,现在从中任意摸出一个红球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com