阅读下面材料：在教学课上，老师提出如下问题：尺规作图：作一条线段的垂直平分线.
已知：线段AB.
求作：线段AB的垂直平分线.
小芸的作法如下：如图， （1）分别以点A和点B为圆心，大于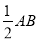
的长为半径作弧，两孤相交于C，D两点； （2）作直线CD.所以直线CD就是所求作的垂直平分线.
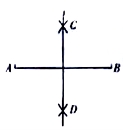
老师说：“小芸的作法正确.”
请回答：小芸的作图依据是____________________，
科目：初中数学 来源：2015年初中毕业升学考试（河南卷）数学（解析版） 题型：解答题
（9分）如图，AB是半圆O的直径，点P是半圆上不与点A、B重合的一个动点，延长BP到点C，使PC=PB，D是AC的中点，连接PD，PO.
（1）求证：△CDP≌△POB；
（2）填空：
① 若AB=4，则四边形AOPD的最大面积为 ；
② 连接OD，当∠PBA的度数为 时，四边形BPDO是菱形.
查看答案和解析>>
科目：初中数学 来源：2015年初中毕业升学考试（北京卷）数学（解析版） 题型：解答题
在平面直角坐标系xOy中，⊙C的半径为r，P是与圆心C不重合的点，点P关于⊙C的反称点的定义如下：若在射线CP上存在一点P′，满足CP＋CP′＝2r.则称P′为点P关于⊙C的反称点，下图为点P及其关于⊙C的反称点P′的示意图.
特别地，当点P′与圆心C重合时，规定CP′＝0.
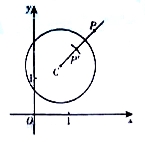
（1）当⊙O的半径为1时.
①分別判断点M（2，1），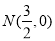
，
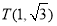关于⊙O的反称点是否存在？若存在，求其坐标；
②点P在直线y＝－x＋2上，若点P关于⊙O的反称点P′存在，且点P′不在x袖上，求点P的横坐标的取值范围；
（2）⊙C的圆心在x袖上，半径为1，直线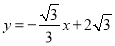
与x轴、y轴分別交于点A，B.若线段AB存在点P，使得点P关于⊙C的反称点P′在⊙C的内部，求圆心C的横坐标的取值范围.
查看答案和解析>>
科目：初中数学 来源：2015年初中毕业升学考试（北京卷）数学（解析版） 题型：解答题
为解决“最后一公里”的交通接驳问题，北京市投放了大量公租自行车供市民使用.到2013年底，全市已有公租自行车25000辆，租赁点600个.预计到2015年底，全市将有公租自行车50000辆，并且平均每个租赁点的公租自行车数量是2013年成平均每个租赁点的公租自行车数量的1.2倍.预计2015年底，全市将租赁点多少个?
查看答案和解析>>
科目：初中数学 来源：2014-2015学年北京市怀柔区中考二模数学试卷（解析版） 题型：填空题
已知等腰△ABC中，AD⊥BC于点D，且AD=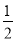
BC，则△ABC底角的度数为__________．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年北京市海淀区中考二模数学试卷（解析版） 题型：选择题
如图，小明将几块六边形纸片分别减掉了一部分（虚线部分），得到了一个新多边形．若新多边形的内角和为540°，则对应的是下列哪个图形（ ）
A．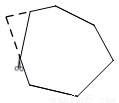
B．
C．
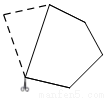D．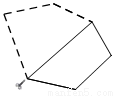
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
，
，则
的大小为 ．
B.
C.
D.