
在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r.则称P′为点P关于⊙C的反称点,下图为点P及其关于⊙C的反称点P′的示意图.
特别地,当点P′与圆心C重合时,规定CP′=0.
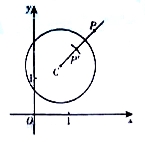
(1)当⊙O的半径为1时.
①分別判断点M(2,1),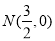 ,
,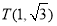 关于⊙O的反称点是否存在?若存在,求其坐标;
关于⊙O的反称点是否存在?若存在,求其坐标;
②点P在直线y=-x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x袖上,求点P的横坐标的取值范围;
(2)⊙C的圆心在x袖上,半径为1,直线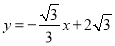 与x轴、y轴分別交于点A,B.若线段AB存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
与x轴、y轴分別交于点A,B.若线段AB存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源:2014-2015学年云南省蒙自市九年级下学期中考一模数学试卷(解析版) 题型:解答题
(7分)兴发服装店老板用4500元购进一批某款T恤衫,由于深受顾客喜爱,很快售完,老板又用4950元购进第二批该款式T恤衫,所购数量与第一批相同,但每件进价比第一批多了9元.
(1)第一批该款式T恤衫每件进价是多少元?
(2)老板以每件120元的价格销售该款式T恤衫,当第二批T恤衫售出 时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价)
时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(河南卷)数学(解析版) 题型:填空题
已知点A(4,y1),B(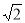 ,y2),C(-2,y3)都在二次函数y=(x-2)2-1的图象上,则y1,y2,y3的大小关系是 .
,y2),C(-2,y3)都在二次函数y=(x-2)2-1的图象上,则y1,y2,y3的大小关系是 .
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(北京卷)数学(解析版) 题型:解答题
如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD//BM,交AB于点F,且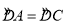 ,连接AC,AD,延长AD交BM于点E.
,连接AC,AD,延长AD交BM于点E.
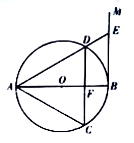
(l)求证:△ACD是等边三角形;
(2)连接OE,若DE=2,求OE的长.
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(北京卷)数学(解析版) 题型:填空题
阅读下面材料:在教学课上,老师提出如下问题:尺规作图:作一条线段的垂直平分线.
已知:线段AB.

求作:线段AB的垂直平分线.
小芸的作法如下:如图, (1)分别以点A和点B为圆心,大于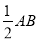 的长为半径作弧,两孤相交于C,D两点; (2)作直线CD.所以直线CD就是所求作的垂直平分线.
的长为半径作弧,两孤相交于C,D两点; (2)作直线CD.所以直线CD就是所求作的垂直平分线.
老师说:“小芸的作法正确.”
请回答:小芸的作图依据是____________________,
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市怀柔区中考二模数学试卷(解析版) 题型:解答题
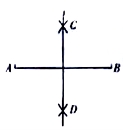
在△ABC内侧作射线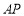 ,自B,C分别向射线AP引垂线,垂足分别为D,E,M为BC边中点,连接MD,ME.
,自B,C分别向射线AP引垂线,垂足分别为D,E,M为BC边中点,连接MD,ME.


(1)依题意补全图1;
(2)求证:MD=ME;
(3)如图2,若射线AP平分∠BAC,且AC>AB,求证:MD=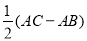 .
.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市海淀区中考二模数学试卷(解析版) 题型:填空题
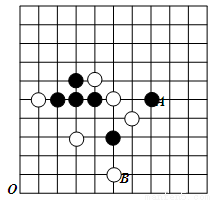
五子棋是一种两人对弈的棋类游戏,规则是:在正方形棋盘中,由黑方先行,白方后行,轮流弈子,下在棋盘横线与竖线的交叉点上,直到某一方首先在任一方向(横向、竖向或者是斜着的方向)上连成五子者为胜.如 图,这一部分棋盘是两个五子棋爱好者的对弈图.观察棋盘,以点O为原点,在棋盘上建立平面直角坐标系,将每个棋子看成一个点,若黑子A的坐标为(7,5),则白子B的坐标为______________;为了不让白方获胜,此时黑方应该下在坐标为______________的位置处.
图,这一部分棋盘是两个五子棋爱好者的对弈图.观察棋盘,以点O为原点,在棋盘上建立平面直角坐标系,将每个棋子看成一个点,若黑子A的坐标为(7,5),则白子B的坐标为______________;为了不让白方获胜,此时黑方应该下在坐标为______________的位置处.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com