
【题目】如图,![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 是⊙
是⊙![]() 上一点,
上一点,![]() 与过点
与过点![]() 的切线垂直,垂足为点
的切线垂直,垂足为点![]() ,直线
,直线![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,弦
,弦![]() 平分∠
平分∠![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
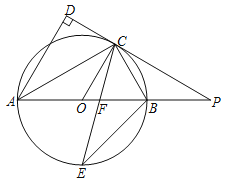
(1)求证:![]() 平分∠
平分∠![]() ;
;
(2)求证:PC=PF;
(3)若![]() ,AB=14,求线段
,AB=14,求线段![]() 的长.
的长.
【答案】(1)证明过程见解析;(2)证明过程见解析;(2)24.
【解析】
试题分析:(1)根据切线以及AD⊥PD得出OC∥AD,得到∠ACO=∠DAC,然后根据OC=OA得出∠ACO=∠CAO,从而得到∠DAC=∠CAO,即角平分线;(2)根据题意得出∠PFC=∠PCF,得出PC=PF;(3)根据题意得出△PAC∽△PCB,根据tan∠ABC可得![]() ,设PC=4k,PB=3k,根据Rt△POC得出PO=3k+7,根据AB的长度得出OC的长度,根据
,设PC=4k,PB=3k,根据Rt△POC得出PO=3k+7,根据AB的长度得出OC的长度,根据![]() 得出k的值,然后求出PC的长度.
得出k的值,然后求出PC的长度.
试题解析:(1)∵PD切⊙O于点C,∴OC⊥PD
又AD⊥PD,∴OC∥AD.∴∠ACO=∠DAC.
又OC=OA,∴∠ACO=∠CAO,
∴∠DAC=∠CAO,即AC平分∠DAB.
(2)∵AD⊥PD,∴∠DAC+∠ACD=90°.
又AB为⊙O的直径,∴∠ACB=90°.
∴∠PCB+∠ACD=90°,
∴∠DAC=∠PCB.
又∠DAC=∠CAO,∴∠CAO=∠PCB.
∵CE平分∠ACB,∴∠ACF=∠BCF,
∴∠CAO+∠ACF=∠PCB+∠BCF,
∴∠PFC=∠PCF,
∴PC=PF
(3)∵∠PAC=∠PCB,∠P=∠P,
∴△PAC∽△PCB,
∴![]() .
.
又tan∠ABC=![]() ,
,
∴![]() ,
,
∴![]()
设![]() ,
,![]() ,则在Rt△POC中,
,则在Rt△POC中,![]() ,
,
∵AB=14,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴k=6 (k=0不合题意,舍去).
∴![]() .
.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°,则下列结论:
①∠BOE=![]() (180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.
(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.
其中正确的个数有多少个?( )
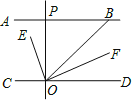
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解中考体育科目训练情况,某县从全县九年级学生中随机抽取了部分学生进行了一次中考体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:

(1)本次抽样测试的学生人数是 ,其中不及格人数占样本人数的百分比为 ;
(2)图1中∠α的度数是 ,并把图2条形统计图补充完整;
(3)测试老师想从4位同学(分别记为E、F、G、H,其中E为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A.(a﹣b)2=a2﹣b2
B.(2a+1)(2a﹣1)=4a﹣1
C.(﹣2a3)2=4a6
D.x2﹣8x+16=(x+4)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条关于数学学习方法的微博在一周内转发了318000次,将318000用科学记数法可以表示为( )
A.3.18×105
B.31.8×105
C.318×104
D.3.18×104
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com