
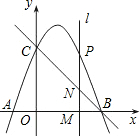
 点,并与x轴交于另一点A.
点,并与x轴交于另一点A.
|
|
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
1+
| ||
| 2 |
1-
| ||
| 2 |
1+
| ||
| 2 |


科目:初中数学 来源: 题型:
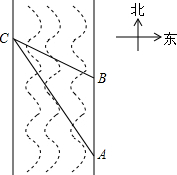 (2012•富宁县模拟)在一次数学活动课上,老师带领学生去测一条南北流向河流的河宽,如图所示,某学生在河东岸点A处观测河对岸水边点C,测得C在A北偏西30°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西60°的方向上.请你根据以上数据,帮助该同学计算出这条河的宽度.(精确到0.1,参考数据:
(2012•富宁县模拟)在一次数学活动课上,老师带领学生去测一条南北流向河流的河宽,如图所示,某学生在河东岸点A处观测河对岸水边点C,测得C在A北偏西30°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西60°的方向上.请你根据以上数据,帮助该同学计算出这条河的宽度.(精确到0.1,参考数据:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 型号 | A | B |
| 成本(万元/台) | 20 | 24 |
| 售价(万元/台) | 25 | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com