
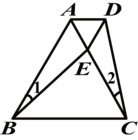 6.如图所示,△ABC是等边三角形,点E是AC上一点,∠
6.如图所示,△ABC是等边三角形,点E是AC上一点,∠
分析:由△ABC是等边三角形,即可得AB=AC,∠BAC=60°,又由∠1=∠2,BE=CD,即可根据SAS判定△ABE≌△ACD,即可得AD=AE,∠CAD=∠BAE=60°,然后由有一个角是60°的等腰三角形是等边三角形,即可判定△ADE是等边三角形.
解答:△ADE是等边三角形.
证明:∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
在△ABE和△ACD中,
| AB=AC ∠1=∠2 BE=CD |
∴△ABE≌△ACB(SAS),
∴AD=AE,∠CAD=∠BAE=60°,
∴△ADE是等边三角形.
点评:此题考查了等边三角形的判定与性质以及全等三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.
题目来源:初中同步测控优化设计八年级数学上册人教版 > 13.3.2等边三角形


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案科目:初中数学 来源: 题型:
18.如图所示是一个工件的横切面,四名同学计算它的面积时,给出了四个答案:
①ab+(a-b)b ; ②
③ ④
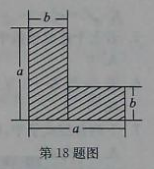
其中正确的有:______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
9.(1)在△ABC中,若∠A=60°,∠B:∠C=2:1,则∠B=___________;
(2)若∠B-∠A=8°,∠C-∠B=56°,则∠C=_____________;
(3)在△ABC中,∠A=105°,∠B-∠C=15°,则∠B=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
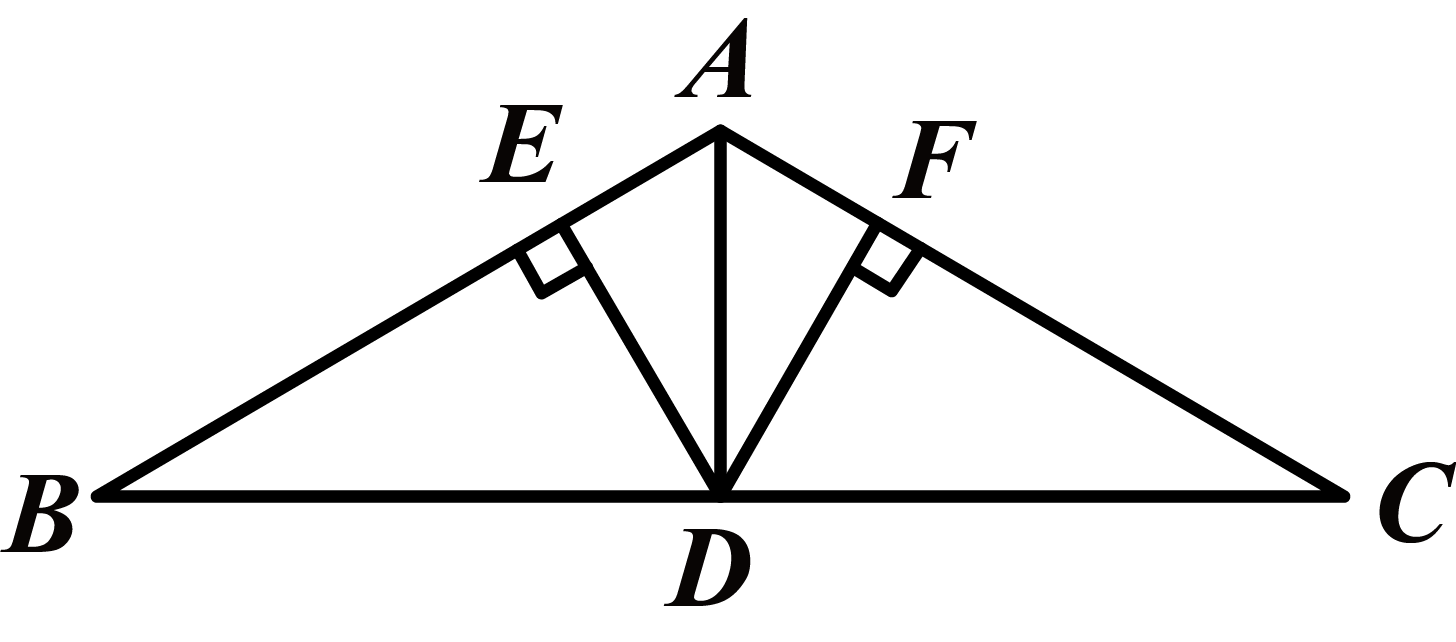 3.如图所示的是屋顶的“人字形”钢架,其中斜梁AB=AC,顶角∠BAC=120°,跨度BC=10 m,AD为柱(即底边BC的中线),两根支撑架DE⊥AB,DF⊥AC,则DE+DF=________.
3.如图所示的是屋顶的“人字形”钢架,其中斜梁AB=AC,顶角∠BAC=120°,跨度BC=10 m,AD为柱(即底边BC的中线),两根支撑架DE⊥AB,DF⊥AC,则DE+DF=________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com