
分析 (1)将an的表达式根据平方差公式计算出来,看是否是8的倍数.
(2)由(1)可得$\sqrt{{a}_{n}}$=$\sqrt{8n}$=2$\sqrt{2n}$,根据该式依次列出所需的完全平方数即可.
解答 解:(1)an不是为6的倍数.
理由:根据平方差公式计算an=(2n+1)2-(2n-1)2=(2n+1-2n+1)(2n+1+2n-1)=8n,
故an是8的倍数,不是6的倍数.
这个结论用文字语言表述为:两个连续奇数的平方差是8的倍数.
(2)∵an=8n,
∴$\sqrt{{a}_{n}}$=$\sqrt{8n}$=2$\sqrt{2n}$,
∴当n分别取2、8、18时得到一列数中从小到大排列的前3个“完全平方数”.
n=2时,an=16,
n=8时,an=64,
n=18时,an=144,
∴这一列数中从小到大排列的前3个“完全平方数”为:16、64、144.
点评 此题考查了完全平方数的知识以及平方差公式的应用.注意利用平方差公式求得an=8n是关键.


科目:初中数学 来源: 题型:填空题
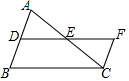 如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得到△CFE,则DF与AC的数量关系是DF=AC.
如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得到△CFE,则DF与AC的数量关系是DF=AC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC中,∠B=90°,AB=11,BC=10,若⊙O的半径为5且与AB、BC相切,以下说法不正确的是①②③.
如图,△ABC中,∠B=90°,AB=11,BC=10,若⊙O的半径为5且与AB、BC相切,以下说法不正确的是①②③.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com