
����Ŀ��̽������
�������ϣ��ѱ�ʾ��1�ĵ��Ϊ���㣬������O������������ͬ��M��N������M�͵�N����O�ľ�����ȣ���Ƶ�M���N��Ϊ���任�㣮���磺ͼ1��MO=NO=2�����M�͵�N��Ϊ���任�㣮
���֣���1����֪��A��ʾ��a����B��ʾ��b����A���B��Ϊ���任�㣮
����a=0����b=�� ������a=4����b=�� ����
���ú�a��ʽ�ӱ�ʾb����b=�� ����
Ӧ�ã���2���Ե�A�������²������Ȱѵ�A��ʾ��������![]() ���ٰ���������ʾ�ĵ��������������ƶ�3����λ���ȵõ���B������A���B��Ϊ���任�����A��ʾ�����Ƕ��٣�
���ٰ���������ʾ�ĵ��������������ƶ�3����λ���ȵõ���B������A���B��Ϊ���任�����A��ʾ�����Ƕ��٣�
̽������3����P������������һ�㣬��Ӧ����Ϊm����P�������²�����P�������������ƶ�k��k��0������λ���ȵõ�P1��P2ΪP1�Ļ��任�㣬��P2�����������ƶ�k����λ���ȵõ���P3����P4ΪP3�Ļ��任�㣬��������˳�ϵ��ظ����õ�P6������������ϵ�P2018��ʾ�����Ƕ��٣����ú�m�Ĵ���ʽ��ʾ��

���𰸡���1����2����2����2��a����2����A��ʾ������2����3����P2018��ʾ����Ϊ2����m+k����
��������
��1���ٸ��ݻ�Ϊ���任��Ķ���ɵó�a+b=2���������ݼ��ɵó����ۣ��ڸ���a+b=2���任�ɵó����ۣ�
��2�����A��ʾ����Ϊx�����ݵ�A���˶��ҳ���B����ϻ�Ϊ���任��Ķ��弴�ɵó�����x��һԪһ�η��̣���֮���ɵó����ۣ�
��3�����ݵ�P�ı仯�ҳ��仯���ɣ�4��һѭ�������������P2018��ʾ����.
��1���١ߵ�A��ʾ��a����B��ʾ��b����A���B��Ϊ���任�㣬
��a+b=2��
��a=0ʱ��b=2����a=4ʱ��b=��2��
�ʴ�Ϊ��2����2��
�ڡ�a+b=2��
��b=2��a��
�ʴ�Ϊ��2��a��
��2�����A��ʾ����Ϊx��
��������ã�![]()
��ã�x=2��
�ʵ�A��ʾ������2��
��3�����P��ʾ����Ϊm���������֪��
P1��ʾ����Ϊm+k��
P2��ʾ����Ϊ2����m+k����
P3��ʾ����Ϊ2��m��
P4��ʾ����Ϊm��
P5��ʾ����Ϊm+k��
��
�ɴ˿ɷ�����4��һѭ����
��2018��4=504��2��
���P2018��ʾ�������P2��ʾ������ͬ��
����P2018��ʾ����Ϊ![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016������ijУ��������ѧ���μ������꼶��ѧ��ĩ���ԣ�ѧУ�����ȡ�˿���������10%��ѧ����ѧ�ɼ����ֽ����ǵijɼ��ֳɣ�A��96�֡�120�֣���B��84�֡�95�֣���C��72�֡�83�֣���D��72�����£��ĸ��ȼ����з����������ݳɼ��õ���������ͳ��ͼ��


��1��������ȡ�Ŀ����У���D��ֻ��3�ˣ�
��������У���п����У�Լ�ж�������ѧ�ɼ���D����
��������ѧ�ɼ�����λ������__________�ȼ��У�
��2����һλͬѧ�ڼ�������ȡ�Ŀ�����ѧ�ɼ���ƽ����ʱ���䷽���ǣ�![]() =
=![]() =76.25��
=76.25��
����λͬѧ�ļ�����ȷ��������ȷ���������������ȷ��ƽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�![]() ��ƽ����
��ƽ����![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() .
.
(1)��ָ��ͼ��ƽ���ı��εĸ�������˵������;
(2)![]() ��
��![]() �����?Ϊʲô?
�����?Ϊʲô?

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ��OB��OM��ON��
��OB��OM��ON��![]() �ڵ����ߣ�
�ڵ����ߣ�
![]() ��ͼ1����OMƽ��
��ͼ1����OMƽ��![]() ��ONƽ��
��ONƽ��![]() ������OB�Ƶ�O��
������OB�Ƶ�O��![]() ����תʱ��
����תʱ��![]() ______��
______��![]()
![]() Ҳ��
Ҳ��![]() �ڵ����ߣ���ͼ2����
�ڵ����ߣ���ͼ2����![]() ��OMƽ��
��OMƽ��![]() ��ONƽ��
��ONƽ��![]() ����
����![]() �Ƶ�O��
�Ƶ�O��![]() ����תʱ����
����תʱ����![]() �Ĵ�С��
�Ĵ�С��
![]() ��
��![]() �������£���
�������£���![]() ����
����![]() ��
��![]() ��O����ÿ��
��O����ÿ��![]() ���ٶ���ʱ����תt�룬��ͼ3����
���ٶ���ʱ����תt�룬��ͼ3����![]() ��
��![]() ��3����t��ֵ��
��3����t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʮһ�ƽ����ڼ䣬��կ��7����ÿ�����������ı仯������±���������ʾ��9��30�ն��������������ʾ��9��30���ٵ���������
���� | 1�� | 2�� | 3�� | 4�� | 5�� | 6�� | 7�� |
�����仯/���� | +0.5 | +0.7 | +0.8 |
|
| +0.2 |
|
(1)�����ж�7�����ο��������������ٵĸ�����һ�죿�������������ˣ���5�֣�
(2)�����9��30����������Ϊ2.5���ˣ�ƽ��ÿ������500Ԫ�����ʷ羰���ڴ�7����������Ϊ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڴ�СΪ4��4�������������У������������ε����������ϱ�ţ��� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�ǵȱ������Σ���ABΪֱ������O����BC���ڵ�D����AC���ڵ�F����DE��AC�ڵ�E�� 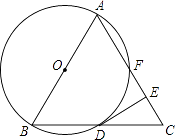
��1����֤��DE�ǡ�O�����ߣ�
��2������ABC�ı߳�Ϊ4����EF�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ����ͼ1����֪A��C����֮��ľ���Ϊ16 cm���ף�������ֱ�����3cm��A��B����ͬʱ������C�㣬�����ٶ�Ϊ8 cm/s���ҵ��ٶ�Ϊ6 cm/s�������˶�ʱ��Ϊx��s���� ��������֮�����Ϊy��cm����
(1)��������ʱ��x = ��
(2)���ú�x�Ĵ���ʽ��ʾy��
��������ǰ��y= ��
�������Һ���C֮ǰ��y= ��
������C֮���ҵ���C֮ǰ��y= ��
![]()
���������ͼ2�����������߶�AC�����������ӱ���Χ��һ���֣��߶�AB���ö�Ӧ�ӱ��ϵĻ�AB��1Сʱ�ļ��������֪��AOB=30����
(1)����ODָ��Բ���ϵĵ���ٶ�Ϊÿ����ת�� cm��ʱ��OEָ��Բ���ϵĵ���ٶ�Ϊÿ����ת�� cm��
(2)����4��00���ʱ�����Ӻ������ʱ���һ���غϣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y=![]() x��˫����y=
x��˫����y=![]() ��k��0������A��B���㣬�ҵ�A�ĺ�����Ϊ4��
��k��0������A��B���㣬�ҵ�A�ĺ�����Ϊ4��

��1���� k��ֵ��
��2������ͼ��ֱ��д������ʽ![]() x��
x��![]() �Ľ⣻
�Ľ⣻
��3����ԭ��O����һ��ֱ��l��˫����y=![]() ��k��0����P��Q���㣨P���ڵ�һ���ޣ������ɵ� A��B��P��QΪ������ɵ��ı������Ϊ 24����� P�����꣮
��k��0����P��Q���㣨P���ڵ�һ���ޣ������ɵ� A��B��P��QΪ������ɵ��ı������Ϊ 24����� P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com