
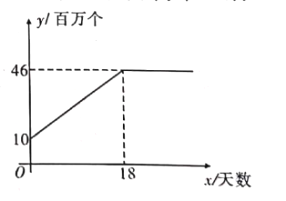
【题目】随着新冠肺炎的爆发,市场对口罩的需求量急剧增大.某口罩生产商自二月份以来,--直积极恢复产能,每日口罩生产量![]() (百万个)与天数
(百万个)与天数![]() 且
且![]() 为整数)的函数关系图象如图所示,而该生产商对口供应市场对口罩的需求量<(百万个)与天数
为整数)的函数关系图象如图所示,而该生产商对口供应市场对口罩的需求量<(百万个)与天数![]() 呈抛物线型,第
呈抛物线型,第![]() 天市场口罩缺口(需求量与供应量差)就达到
天市场口罩缺口(需求量与供应量差)就达到![]() (百万个),之后若干天,市场口罩需求量不断上升,在第
(百万个),之后若干天,市场口罩需求量不断上升,在第![]() 天需求量达到最高峰
天需求量达到最高峰![]() (百万个).
(百万个).
![]() 求出
求出![]() 与
与![]() 的函数解析式;
的函数解析式;
![]() 当市场供应量不小于需求量时,市民买口罩才无需提前预约,那么在整个二月份,市民无需预约即可购买口罩的天数共有多少天?
当市场供应量不小于需求量时,市民买口罩才无需提前预约,那么在整个二月份,市民无需预约即可购买口罩的天数共有多少天?
【答案】(1)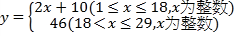 ;(2)在整个二月份,市民无需预约即可购买到口罩的天数共有
;(2)在整个二月份,市民无需预约即可购买到口罩的天数共有![]() 天.
天.
【解析】
(1)根据函数图象,结合待定系数法分段求解即可;
(2)根据题意设出抛物线顶点式,求出第一天口罩需求量,进而求出抛物线解析式,然后根据一次函数及二次函数的性质解答即可.
解:(1)当![]() 时,设
时,设![]() ,
,
把![]() ,
,![]() 代入,得
代入,得![]() ,解得
,解得![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,
,
综上所述,![]() ;
;
![]() 由题意可设该生产商对口供应市场对口罩的需求量
由题意可设该生产商对口供应市场对口罩的需求量![]() ,
,
当![]() 时,代入
时,代入![]() 得
得![]() ,
,
此时口罩需求量为![]() (百万个),
(百万个),
将![]() 代入
代入![]() 中,得
中,得![]() ,
,
解得:![]() ,
,
所以![]() ,
,
当![]() 时,令
时,令![]() ,即
,即![]() ,
,
解得:![]() (舍去),
(舍去),![]() ,即此时需求和供应平衡,均为
,即此时需求和供应平衡,均为![]() 百万个,
百万个,
当![]() 时,
时,![]() 随着
随着![]() 增大而增大,
增大而增大,
故![]() ;
;
当![]() 时,
时,![]() ;
;
且当![]() 时,
时,![]() 随着
随着![]() 增大而减小,
增大而减小,
所以![]() ,
,
综上所述,从第![]() 天开始,
天开始,![]() ,
,
![]() (天),
(天),
答:在整个二月份,市民无需预约即可购买到口罩的天数共有![]() 天.
天.


科目:初中数学 来源: 题型:
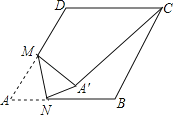
【题目】如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办学生综合素质大赛,分“单人项目”和“双人项目”两种形式,比赛题目包括下列五类:![]() .人文艺术;
.人文艺术;![]() .历史社会;
.历史社会;![]() .自然科学;
.自然科学;![]() .天文地理;
.天文地理;![]() .体育健康.
.体育健康.
(1)若小明参加“单人项目”,他从中抽取一个题目,那么恰好抽中“自然科学”类题目的概率为_____.
(2)小林和小丽参加“双人项目”,比赛规定:同一小组的两名同学的题目类型不能相同,且每人只能抽取一次,求他们抽到“天文地理”和“体育健康”类题目的概率是多少?(用画树状图或列表的方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
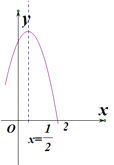
【题目】如图是二次函数![]() 图象的一部分,对称轴为
图象的一部分,对称轴为![]() ,且经过点
,且经过点![]() ,有下列说法:①
,有下列说法:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() 是抛物线上的两点,则
是抛物线上的两点,则![]() ,上述说法正确的是( )
,上述说法正确的是( )
A.①②④B.③④C.①③④D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=![]() HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,点A(2,1).
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点P,使四边形ABOP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 和
和![]() .
.![]() 是由
是由![]() 经过一系列变化得到的.
经过一系列变化得到的.
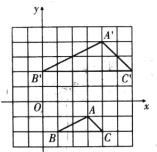
(1)请通过作图说明![]() 经过怎样的变化可以得到
经过怎样的变化可以得到![]() ;
;
(2)若![]() 为
为![]() 内任一点,则它的对应点
内任一点,则它的对应点![]() 的坐标为 .
的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com