
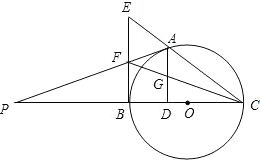
 如图,点A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P,且FG=FB=3.则以下四个结论:①BF=EF;②PA⊥OA;③tan∠P=$\frac{{\sqrt{2}}}{3}$;④OC=3$\sqrt{2}$,上述结论中正确的有①②④(填番号).
如图,点A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P,且FG=FB=3.则以下四个结论:①BF=EF;②PA⊥OA;③tan∠P=$\frac{{\sqrt{2}}}{3}$;④OC=3$\sqrt{2}$,上述结论中正确的有①②④(填番号). 分析 ①正确,根据AD∥EB得$\frac{AG}{EF}=\frac{CG}{CF}=\frac{GD}{BF}$即可证明.②正确,只要证明∠FAB+∠OAB=90°即可.③错误,求出AH,FH,根据tan∠P=tan∠AFH=$\frac{AH}{FH}$=$\frac{1}{2\sqrt{2}}$=$\frac{\sqrt{2}}{4}$,即可解决问题.④正确,在RT△ADO中利用勾股定理即可求出半径.
解答 解:如图连接AO、AB、BG作FH⊥AD于H,
∵EB是切线,AD⊥BC
∴∠EBC=∠ADC=90°,
∴AD∥EB,
∴$\frac{AG}{EF}=\frac{CG}{CF}=\frac{GD}{BF}$,
∵AG=GD,
∴EF=FB故①正确,
∵BC是直径,
∴∠BAC=∠BAE=90°,∵EF=FB,
∴FA=FB=FE=FG=3,
∴∠FAB=∠FBA,
∵OA=OB,
∴∠OAB=∠OBA,
∵∠FBA+∠ABO=90°,
∴∠FAB+∠OAB=90°,
∴PA是⊙O的切线,故②正确.
∵FA=FG,FH⊥AG,
∴AH=HG,
∵∠FBD=∠BDH=∠FHD=90°,
∴四边形FBDH是矩形,
∴FB=DH=3,
∵AG=GD,
∴AH=HG=1,GD=2,FH=$\sqrt{A{F}^{2}-A{H}^{2}}$=2$\sqrt{2}$,
∵FH∥PD,
∴∠AFH=∠APD,
∴tan∠P=tan∠AFH=$\frac{AH}{FH}$=$\frac{1}{2\sqrt{2}}$=$\frac{\sqrt{2}}{4}$,故③错误,
设半径为r,在RT△ADO中,∵AO2=AD2+OD2,
∴r2=42+(r-2$\sqrt{2}$)2,
∴r=3$\sqrt{2}$故④正确,
故答案为①②④.
点评 本题考查圆的有关知识、平行线分线段成比例定理、直角三角形斜边中线定理、勾股定理等知识,解题的关键是添加常用辅助线,体现了转化的思想,把问题转化为方程解决,属于中考压轴题.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知在四边形ABCD中,AD∥BC,对角线AC、BD相交于点O,BD平分∠ABC,过点D作DF∥AB分别交AC、BC于点E、F.
如图,已知在四边形ABCD中,AD∥BC,对角线AC、BD相交于点O,BD平分∠ABC,过点D作DF∥AB分别交AC、BC于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=6}\\{y=-5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=-\frac{5}{2}}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=8}\\{y=10}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5}\\{y=-\frac{11}{2}}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{BC}$,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是( )
如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{BC}$,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是( )| A. | $\frac{5}{3}π-2\sqrt{3}$ | B. | $\frac{5}{3}π+2\sqrt{3}$ | C. | 2$\sqrt{3}-\frac{5}{3}π$ | D. | $\sqrt{3}+\frac{5}{3}π$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com