
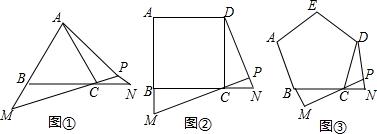
分析 探究:(1)利用等边三角形的性质得到BC=AC,∠ACB=∠ABC,从而得到△ACN≌△CBM.
(2)利用全等三角形的性质得到∠CAN=∠BCM,再利用三角形的外角等于与它不相邻的两内角之和,即可求解.
应用:利用正方形(或正五边形)的性质得到BC=DC,∠ABC=∠BCD,从而判断出△DCN≌△CBM,再利用全等三角形的性质得到∠CDN=∠BCM,再利用三角形的外角等于与它不相邻的两内角之和(或者三角形的内角和),即可.
拓展:利用正n五边形的性质得到BC=DC,∠ABC=∠BCD,从而判断出△DCN≌△CBM,再利用全等三角形的性质得到∠CDN=∠BCM,再利用三角形的内角和,即可.
解答 探究:(1)解:∵△ABC是等边三角形,
∴BC=AC,∠ACB=∠ABC=60°.
∴∠ACN=∠CBM=60°.
在△ACN和△CBM中,
$\left\{\begin{array}{l}{∠ACN=∠CBM}\\{∠ACB=∠ABC}\\{BM=CN}\end{array}\right.$
∴△ACN≌△CBM.
(2)解:∵△DCN≌△CBM,
∴∠CAN=∠BCM,
∵∠ABC=∠BMC+∠BCM,∠BAN=∠BAC+∠CAN,
∴∠CPN=∠BMC+∠BAN=∠BMC+∠BAC+∠CAN=∠BMC+∠BAC+∠BCM=∠ABC+∠BAC=60°+60°=120°,
故答案为120.
应用:将等边三角形换成正方形,
解:四边形ABCD是正方形,
∴BC=DC,∠ABC=∠BCD=90°.
∴∠MBC=∠DCN=120°.
在△DCN和△CBM中,
$\left\{\begin{array}{l}{∠ABC=∠BCD}\\{∠MBC=∠DCN}\\{BM=CN}\end{array}\right.$
∴△DCN≌△CBM.
∴∠CDN=∠BCM,
∵∠BCM=∠PCN
∴∠CDN=∠PCN
在Rt△DCN中,∠CDN+∠CND=90°,
∴∠PCN+∠CND=90°,
∴∠CPN=90,
将等边三角形换成正五边形,
五边形ABCDE是正五边形,
∴BC=DC=108°.
∴∠MBC=∠DCN=72°.
在△DCN和△CBM中,
$\left\{\begin{array}{l}{∠ABC=∠BCD}\\{∠MBC=∠DCN}\\{BM=CN}\end{array}\right.$
∴△DCN≌△CBM.
∴∠BMC=∠CND,∠BCM=∠CDN,
∵∠ABC=∠BMC+∠BCM=108°
∴∠CPN=180°-(∠CND+∠PCN)=180°-(∠CND+∠BCM)=180°-(∠BCM+∠BMC)=180°-108°=72°.
故答案为90,72.
拓展
解:方法和上面正五边形的方法一样,得到∠CPN=180°-(∠CND+∠PCN)=180°-(∠CND+∠BCM)=180°-(∠BCM+∠BMC)=180°-108°=72°
故答案为$\frac{360}{n}$.
点评 本题是四边形的综合题,也是一道规律题,主要考查了正n边形的性质,涉及知识点比较多,如等边三角形、正方形、正五边形的性质,如由四边形ABCD是正方形,得到BC=DC,∠ABC=∠BCD=90°,全等三角形的性质和判定,三角形的内角和定理,对顶角相等,解题的关键是充分利用三角形的外角等于与它不相邻的两内角之和(或者三角形的内角和).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 甲、乙两车分别从M,N两地沿同一公路相向匀速行驶,两车分别抵达N,M两地后即停止行驶.已知乙车比甲车提前出发,设甲、乙两车之间的路程S(km),乙行驶的时间为t(h),S与t的函数关系如图所示.有下列说法:
甲、乙两车分别从M,N两地沿同一公路相向匀速行驶,两车分别抵达N,M两地后即停止行驶.已知乙车比甲车提前出发,设甲、乙两车之间的路程S(km),乙行驶的时间为t(h),S与t的函数关系如图所示.有下列说法:| A. | ①② | B. | ②③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
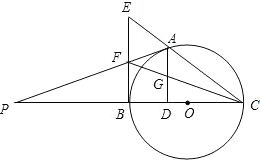 如图,点A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P,且FG=FB=3.则以下四个结论:①BF=EF;②PA⊥OA;③tan∠P=$\frac{{\sqrt{2}}}{3}$;④OC=3$\sqrt{2}$,上述结论中正确的有①②④(填番号).
如图,点A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P,且FG=FB=3.则以下四个结论:①BF=EF;②PA⊥OA;③tan∠P=$\frac{{\sqrt{2}}}{3}$;④OC=3$\sqrt{2}$,上述结论中正确的有①②④(填番号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com