
【题目】一段抛物线C:y=﹣x2+3x+m(0≤x≤3)与直线y=x+1有唯一公共点,若m为整数,则符合条件的所有m的值的和为_____.
【答案】9
【解析】
分两种情况进行讨论,①当抛物线与直线相切,△=0求得m=0,②当抛物线与直线不相切,但在0≤x≤3上只有一个交点时,找到两个临界值点,可得m=2,3,4,故m=0,2,3,4,然后求得它们的和即可.
解:∵抛物线C:y=﹣x2+3x+m(0≤x≤3)与直线y=x+1有唯一公共点
∴①如图1,抛物线与直线相切,
联立解析式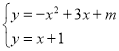 得x2﹣2x+1﹣m=0
得x2﹣2x+1﹣m=0
△=(﹣2)2﹣4(1﹣m)=0
解得m=0
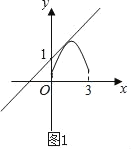
②如图2,抛物线与直线不相切,但在0≤x≤3上只有一个交点
此时两个临界值分别为(0,1)和(3,4)在抛物线上,
∴m的最小值=1,但取不到,c的最大值=4,能取到,
∴1<m≤4,
又∵m为整数,
∴m=2,3,4,
综上,m=0,2,3,4,
0+2+3+4=9,
故答案为9.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
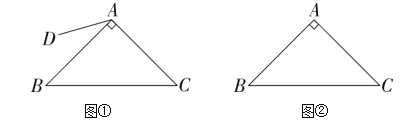
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.在平面内任取一点D,连接AD(AD<AB),将线段AD绕点A逆时针旋转90°得到线段AE,连接DE,CE,BD.
(1)请根据题意补全图①;
(2)猜测BD和CE的数量关系并证明;
(3)作射线BD,CE交于点P,把△ADE饶点A旋转,当∠EAC=90°,AB=3,AD=2时,补全图形,直接写出PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每位同学都能感受到日出时美丽的景色.下图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A﹑B两点,他测得“图上”圆的半径为5厘米,AB=8厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为16分钟,求“图上”太阳升起的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣6,0)、B(2,0)、C(0,6)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足为点E,连接AE.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果点P的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)过点P(﹣3,m)作x轴的垂线,垂足为点F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P,求出P的坐标.(直接写出结果)
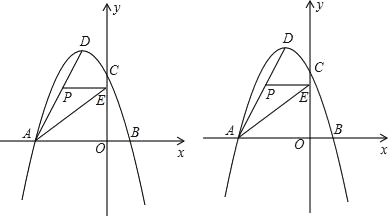
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A在x轴上,点B在第一象限内,∠OAB=90°,OA=AB,△OAB的面积为2,反比例函数y=![]() 的图象经过点B.
的图象经过点B.
(1)求k的值;
(2)已知点P坐标为(a,0),过点P作直线OB的垂线l,点O,A关于直线l的对称点分别为O′,A′,若线段O′A′与反比例函数y=![]() 的图象有公共点,直接写出a的取值范围.
的图象有公共点,直接写出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.
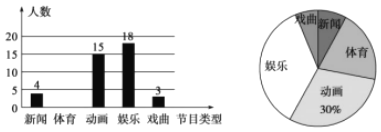
请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?
(2)请将条形统计图补充完整;
(3)若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?
(4)该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
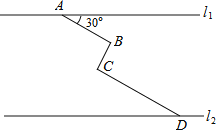
【题目】如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形![]() 位似,位似比
位似,位似比![]() =2,四边形A′B′C′D′和四边形
=2,四边形A′B′C′D′和四边形![]() 位似,位似比
位似,位似比![]() =1.四边形
=1.四边形![]() 和四边形ABCD是位似图形吗?位似比是多少?
和四边形ABCD是位似图形吗?位似比是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】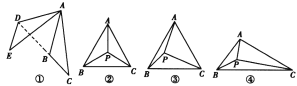
(1)(操作发现)
如图①,将△ABC绕点A顺时针旋转60°,得到△ADE,连接BD,则∠ABD=____度;
(2)(类比探究)
如图②,在等边三角形ABC内任取一点P,连接PA,PB,PC,求证:以PA,PB,PC的长为三边必能组成三角形:
(3)(解决问题)
如图③,在边长为![]() 的等边三角形ABC内有一点P,∠APC=90°,∠BPC=120°,求△APC的面积;
的等边三角形ABC内有一点P,∠APC=90°,∠BPC=120°,求△APC的面积;
(4)(拓展应用)
图④是A,B,C三个村子位置的平面图,经测量AC=4,BC=5,∠ACB=30°,P为△ABC内的一个动点,连接PA,PB,PC,求PA+PB+PC的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com