
【题目】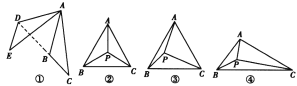
(1)(操作发现)
如图①,将△ABC绕点A顺时针旋转60°,得到△ADE,连接BD,则∠ABD=____度;
(2)(类比探究)
如图②,在等边三角形ABC内任取一点P,连接PA,PB,PC,求证:以PA,PB,PC的长为三边必能组成三角形:
(3)(解决问题)
如图③,在边长为![]() 的等边三角形ABC内有一点P,∠APC=90°,∠BPC=120°,求△APC的面积;
的等边三角形ABC内有一点P,∠APC=90°,∠BPC=120°,求△APC的面积;
(4)(拓展应用)
图④是A,B,C三个村子位置的平面图,经测量AC=4,BC=5,∠ACB=30°,P为△ABC内的一个动点,连接PA,PB,PC,求PA+PB+PC的最小值.
【答案】(1)60,理由见解析;(2)见解析;(3)![]() ;(4)
;(4)![]()
【解析】
(1)【操作发现】:如图1中,只要证明△DAB是等边三角形即可;
(2)【类比探究】:如图2中,以PA为边长作等边△PAD,使P、D分别在AC的两侧,连接CD.利用全等三角形的性质以及三角形的三边关系即可解决问题;
(3)【解决问题】:如图3中,将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,只要证明∠PP′C=90°,利用勾股定理即可解决问题;
(4)【拓展应用】:如图4中,先由旋转的性质得出△APC≌△EDC,则∠ACP=∠ECD,AC=EC=4,∠PCD=60°,再证明∠BCE=90°,然后在Rt△BCE中,由勾股定理求出BE的长度,即为PA+PB+PC的最小值;
(1)【操作发现】60.
理由:∵△ABC绕点A顺时针旋转60°,得到△ADE,∴AD=AB,∠DAB=60°,∴△DAB是等边三角形,∴∠ABD=60°.
(2)【类比探究】证明:如图,以PA为边长作等边△PAD,使 P,D分别在,AC的两侧,连接CD.
∵∠BAC=∠PAD=60°
∴∠BAP=∠CAD.
∵AB=AC,AP=AD,
∴△PAB≌△DAC(SAS),
∴BP=CD.
在△PCD中,∵PD+CD>PC.
又∵AP=PD,
∴AP+BP>PC.
∴以PA,PB,PC的长为三边必能组成三角形.
(3)【解决问题】如图,将△APB绕点A按逆时针方向旋转60°,得到△AP′C,
∴∠AP′C=∠APB=360°-90°-120°=150°,
AP=AP′,∠PAP′= 60∴△APP′是等边三角形,
∴PP′=AP,∠AP′P=∠APP′=60°,
∴∠PP′C=150°-60°=90°, ∠P′PC=∠APC-∠APP′=30°,
∴PP′=![]() ,即AP=
,即AP=![]() .
.
∵∠APC=90°,AC=![]() ,
,
∴AP +PC =AC,即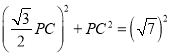 ,
,
∴PC=2(舍负),∴AP=![]() ,∴
,∴![]() .
.
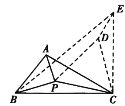
(4)【拓展应用】如图,将△APC绕点C顺时针旋转60°,得到△EDC,连接PD,BE.
∵将△APC绕点C顺时针旋转60°得到△EDC,
∴△APC≌△EDC,∠PCD=60°
∴∠ACP=∠ECD,AC=EC=4,
∴∠ACB=∠ACP+∠PCB=∠ECD+∠PCB=30°,
∴∠BCE=∠ECD+∠PCB+∠PCD=30°+60°=90°.
在Rt△BCE中,∵BC=5,CE=4,
∴![]() ,
,
当P,D在BE上时,PA+PB+PC=BE,此时PA+PB+PC取最小值,为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
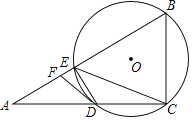
【题目】如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,过B,C,D三点的⊙O交AB于点E,连接ED,EC,点F是线段AE上的一点,连接FD,其中∠FDE=∠DCE.
(1)求证:DF是⊙O的切线.
(2)若D是AC的中点,∠A=30°,BC=4,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
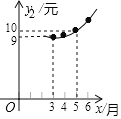
【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |
(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x+2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象,如图.在这个新图象上有一点P,能使得S△ABP=6,则点P的坐标为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
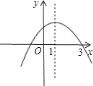
【题目】已知二次函数![]() 的图象如图所示,则关于
的图象如图所示,则关于![]() 的一元二次方程
的一元二次方程![]() 的根为________;不等式
的根为________;不等式![]() 的解集是________;当
的解集是________;当![]() ________时,
________时,![]() 随
随![]() 的增大而减小.
的增大而减小.
查看答案和解析>>
科目:初中数学 来源: 题型:
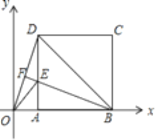
【题目】如图,在平面直角坐标系中,边长为![]() 的正方形ABCD的顶点A,B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E,连接OE,若点M是直线BF上的一动点,且△BMD与△OED相似,则点M的坐标_____.
的正方形ABCD的顶点A,B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E,连接OE,若点M是直线BF上的一动点,且△BMD与△OED相似,则点M的坐标_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明在网上经营一家水果店,销售的草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒。为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元。每笔订单顾客网上支付成功后,李明会得到支付款的80%。在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为_________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com