
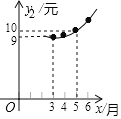
【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |
(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?
【答案】(1)y1=2x+6;(2)y2=![]() x2﹣
x2﹣![]() x+
x+![]() ;(3)w=﹣
;(3)w=﹣![]() x2+
x2+![]() x﹣
x﹣![]() ,7月份销售每千克猪肉所第获得的利润最大,最大利润是77元7.
,7月份销售每千克猪肉所第获得的利润最大,最大利润是77元7.
【解析】
(1)设![]() 与x之间的函数关系式为
与x之间的函数关系式为![]() ,将(3,12)(4,14)代入
,将(3,12)(4,14)代入![]() 解方程组即可得到结论;
解方程组即可得到结论;
(2)由题意得到抛物线的顶点坐标为(3,9),设![]() 与x之间的函数关系式为:
与x之间的函数关系式为:![]() =
=![]() ,将(5,10)代入
,将(5,10)代入![]() =
=![]() 得
得![]() =10,解方程即可得到结论;
=10,解方程即可得到结论;
(3)由题意得到w=![]()
![]() =2x+6
=2x+6![]()
![]() +
+![]() x
x![]() =
=![]()
![]() +
+![]() x
x![]() ,根据二次函数的性质即可得到结论.
,根据二次函数的性质即可得到结论.
(1)设y1与x之间的函数关系式为y1=kx+b,
将(3,12)(4,14)代入y1得,![]() ,
,
解得:![]() ,
,
∴y1与x之间的函数关系式为:y1=2x+6;
(2)由题意得,抛物线的顶点坐标为(3,9),
∴设y2与x之间的函数关系式为:y2=a(x﹣3)2+9,
将(5,10)代入y2=a(x﹣3)2+9得a(5﹣3)2+9=10,
解得:a=![]() ,
,
∴y2=![]() (x﹣3)2+9=
(x﹣3)2+9=![]() x2﹣
x2﹣![]() x+
x+![]() ;
;
(3)由题意得,w=y1﹣y2=2x+6﹣![]() x2+
x2+![]() x﹣
x﹣![]() =﹣
=﹣![]() x2+
x2+![]() x﹣
x﹣![]() ,
,
∵﹣![]() <0,
<0,
∴w由最大值,
∴当x=﹣![]() =﹣
=﹣ =7时,w最大=﹣
=7时,w最大=﹣![]() ×72+
×72+![]() ×7﹣
×7﹣![]() =7span>.
=7span>.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣6,0)、B(2,0)、C(0,6)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足为点E,连接AE.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果点P的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)过点P(﹣3,m)作x轴的垂线,垂足为点F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P,求出P的坐标.(直接写出结果)
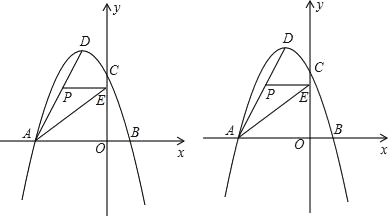
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形![]() 位似,位似比
位似,位似比![]() =2,四边形A′B′C′D′和四边形
=2,四边形A′B′C′D′和四边形![]() 位似,位似比
位似,位似比![]() =1.四边形
=1.四边形![]() 和四边形ABCD是位似图形吗?位似比是多少?
和四边形ABCD是位似图形吗?位似比是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
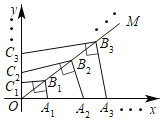
【题目】如图,点A1,A2,A3…,An在x轴正半轴上,点C1,C2,C3,…,![]() 在y轴正半轴上,点B1,B2,B3,…,Bn在第一象限角平分线OM上,OB1=B1B2=B1B3=…=Bn﹣1Bn=
在y轴正半轴上,点B1,B2,B3,…,Bn在第一象限角平分线OM上,OB1=B1B2=B1B3=…=Bn﹣1Bn=![]() a,A1B1⊥B1C1,A2B2⊥B2C2,A3B3⊥B3C3,…,
a,A1B1⊥B1C1,A2B2⊥B2C2,A3B3⊥B3C3,…,![]() ,…,则第n个四边形
,…,则第n个四边形![]() 的面积是____.
的面积是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
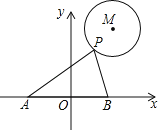
A. 3B. 4C. 6D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】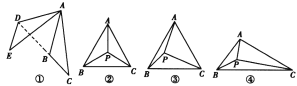
(1)(操作发现)
如图①,将△ABC绕点A顺时针旋转60°,得到△ADE,连接BD,则∠ABD=____度;
(2)(类比探究)
如图②,在等边三角形ABC内任取一点P,连接PA,PB,PC,求证:以PA,PB,PC的长为三边必能组成三角形:
(3)(解决问题)
如图③,在边长为![]() 的等边三角形ABC内有一点P,∠APC=90°,∠BPC=120°,求△APC的面积;
的等边三角形ABC内有一点P,∠APC=90°,∠BPC=120°,求△APC的面积;
(4)(拓展应用)
图④是A,B,C三个村子位置的平面图,经测量AC=4,BC=5,∠ACB=30°,P为△ABC内的一个动点,连接PA,PB,PC,求PA+PB+PC的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com