
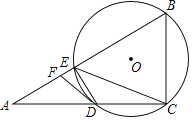
【题目】如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,过B,C,D三点的⊙O交AB于点E,连接ED,EC,点F是线段AE上的一点,连接FD,其中∠FDE=∠DCE.
(1)求证:DF是⊙O的切线.
(2)若D是AC的中点,∠A=30°,BC=4,求DF的长.
【答案】(1)见解析;(2)DF=![]() .
.
【解析】
(1)可证得BD是⊙O的直径,∠BCE=∠BDE,则∠BDE+∠FDE=90°,结论得证;
(2)先求出AC长,再求DE长,在Rt△BCD中求出BD长,在Rt△BED中求出BE长,证得△FDE∽△DBE,由比例线段![]() 可求出DF长.
可求出DF长.
解:(1)∵∠ACB=90°,点B,D在⊙O上,
∴BD是⊙O的直径,∠BCE=∠BDE,
∵∠FDE=∠DCE,∠BCE+∠DCE=∠ACB=90°,
∴∠BDE+∠FDE=90°,
即∠BDF=90°,
∴DF⊥BD,
又∵BD是⊙O的直径,
∴DF是⊙O的切线.
(2)如图,∵∠ACB=90°,∠A=30°,BC=4,
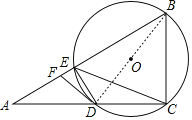
∴AB=2BC=2×4=8,
∴![]() ,
,
∵点D是AC的中点,
∴![]() ,
,
∵BD是⊙O的直径,
∴∠DEB=90°,
∴∠DEA=180°﹣∠DEB=90°,
∴![]() ,
,
在Rt△BCD中, ![]() ,
,
在Rt△BED中,![]() ,
,
∵∠FDE=∠DCE,∠DCE=∠DBE,
∴∠FDE=∠DBE,
∵∠DEF=∠BED=90°,
∴△FDE∽△DBE,
∴![]() ,即
,即![]() ,
,
∴![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】某校为调查“停课不停学”期间九年级学生平均每天上网课时长,随机抽取了![]() 名九年级学生做网络问卷调查.共四个选项:
名九年级学生做网络问卷调查.共四个选项:![]() 小时以下)、
小时以下)、![]() 小时)、
小时)、![]() 小时),
小时), ![]() 小时以上),每人只能选一
小时以上),每人只能选一
项.并将调查结果绘制成如下不完整的统计表和统计图.
被调查学生平均每天上网课时间统计表
时长 | 所占百分比 |
|
|
|
|
|
|
|
|
合计 |
|
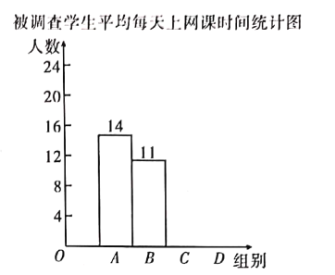
根据以上信息,解答下列问题:
![]() ,
,![]() ,
,
![]() 补全条形统计图;
补全条形统计图;
![]() 该校有九年级学生
该校有九年级学生![]() 名,请你估计仝校九年级学生平均每天上网课时长在
名,请你估计仝校九年级学生平均每天上网课时长在![]() 小时及以上的共多少名;
小时及以上的共多少名;
![]() 在被调查的对象中,平均每天观看时长超过
在被调查的对象中,平均每天观看时长超过![]() 小时的,有
小时的,有![]() 名来自九
名来自九![]() 班,
班,![]() 名来自九
名来自九![]() 班,其余都来自九
班,其余都来自九![]() 班,现教导处准备从
班,现教导处准备从![]() 选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的
选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的![]() 名学生恰好来自同一个班级的概率.
名学生恰好来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 上一点,点
上一点,点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 的切线,与
的切线,与![]() 、
、![]() 的延长线分别交于点
的延长线分别交于点![]() 、
、![]() ,连接
,连接![]() .
.
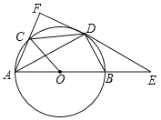
(1)求证:![]() ;
;
(2)直接回答:①已知![]() ,当
,当![]() 为何值时,
为何值时,![]() ?
?
②连接![]() 、
、![]() 、
、![]() ,当
,当![]() 等于多少度时,四边形
等于多少度时,四边形![]() 是菱形?
是菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
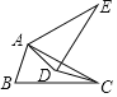
【题目】如图,在△ABC中,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,若AB=2,∠ACB=30°,则线段CD的长度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
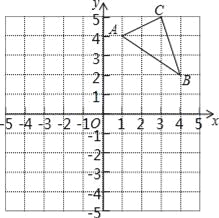
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
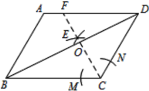
【题目】如图,在平行四边形ABCD中,AB=4,BC=5,∠ABC=60°. 按以下步骤作图:①以C为圆心,以适当长为半径做弧,交CB、CD于M、N两点;②分别以M、N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点E,作射线CE交BD于点O,交AD边于点F;则BO的长度为( )
MN的长为半径作弧,两弧相交于点E,作射线CE交BD于点O,交AD边于点F;则BO的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
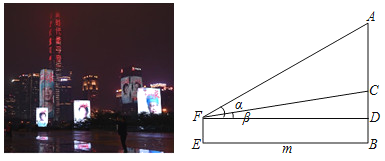
【题目】2020年3月20日,深圳市民中心及周边楼宇为当日返回深圳的援鄂医疗队员亮灯,欢迎最美逆行者回家.小洪在欢迎英雄回家现场,如图,若他观测到英雄画像电子屏顶端A和底端C的仰角分别为∠α和∠β,小洪所站位置E到电子屏边缘AC垂直地面的B点距离为m米,那么英雄画像电子屏高AC为( )
A.![]() 米B.mtan(α﹣β)米
米B.mtan(α﹣β)米
C.m(tanα﹣tanβ)米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两张完全重合的矩形纸片,将其中一张绕点![]() 顺时针旋转
顺时针旋转![]() 后得到矩形
后得到矩形![]() (如图1),连接
(如图1),连接![]() ,
,![]() ,若
,若![]() ,
,![]() .
.

(1)试探究线段![]() 与线段
与线段![]() 的数量关系和位置关系,并说明理由;
的数量关系和位置关系,并说明理由;
(2)把![]() 与
与![]() 剪去,将
剪去,将![]() 绕点
绕点![]() 顺时针旋转得
顺时针旋转得![]() ,边
,边![]() 交
交![]() 于点
于点![]() (如图2),设旋转角为
(如图2),设旋转角为![]() ,当
,当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的度数;
的度数;
(3)若将![]() 沿
沿![]() 方向平移得到
方向平移得到![]() (如图3),
(如图3),![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 时,求平移的距离.
时,求平移的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com