
【题目】有两张完全重合的矩形纸片,将其中一张绕点![]() 顺时针旋转
顺时针旋转![]() 后得到矩形
后得到矩形![]() (如图1),连接
(如图1),连接![]() ,
,![]() ,若
,若![]() ,
,![]() .
.

(1)试探究线段![]() 与线段
与线段![]() 的数量关系和位置关系,并说明理由;
的数量关系和位置关系,并说明理由;
(2)把![]() 与
与![]() 剪去,将
剪去,将![]() 绕点
绕点![]() 顺时针旋转得
顺时针旋转得![]() ,边
,边![]() 交
交![]() 于点
于点![]() (如图2),设旋转角为
(如图2),设旋转角为![]() ,当
,当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的度数;
的度数;
(3)若将![]() 沿
沿![]() 方向平移得到
方向平移得到![]() (如图3),
(如图3),![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 时,求平移的距离.
时,求平移的距离.
【答案】(1)![]() ,
,![]() ,理由见解析;(2)
,理由见解析;(2)![]() 或
或![]() ;(3)平移的距离是
;(3)平移的距离是![]()
【解析】
(1)有两张完全重合的矩形纸片,将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),得BD=MF,△BAD≌△MAF,推出BD=MF,∠ADB=∠AFM=30°,进而可得∠DNM的大小.
(2)分两种情形讨论①当AK=FK时,②当AF=FK时,根据旋转的性质得出结论.
(3)求平移的距离是A2A的长度.在矩形PNA2A中,A2A=PN,只要求出PN的长度就行.用△DPN∽△DAB得出对应线段成比例,即可得到A2A的大小.
(1)解:![]() ,
,![]() .
.
延长![]() 交
交![]() 于点
于点![]() ,
,

根据旋转的性质得:AB=AM,AD=AF,∠BAD=∠MAF=90°
∴![]() .
.
∴![]() ,
,![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
(2)解:如图2,

①当![]() 时,
时,![]() ,
,
则![]() ,即
,即![]() ;
;
②当![]() 时,
时,![]() ,
,
∴![]() ,即
,即![]() ;
;
∴![]() 的度数为
的度数为![]() 或
或![]()
(3)如图3,
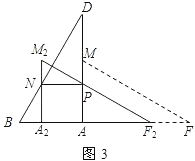
由题意得矩形![]() .设
.设![]() ,则
,则![]() ,
,
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴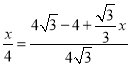 ,
,
解得![]() .即
.即![]() .
.
答:平移的距离是![]() .
.


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:
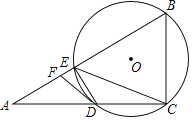
【题目】如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,过B,C,D三点的⊙O交AB于点E,连接ED,EC,点F是线段AE上的一点,连接FD,其中∠FDE=∠DCE.
(1)求证:DF是⊙O的切线.
(2)若D是AC的中点,∠A=30°,BC=4,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
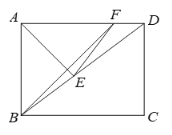
【题目】如图,在矩形ABCD中,AB=6,BC=8,点E是对角线BD上的一点,把△ABE沿着直线AE翻折得到△AFE,且点F恰好落在AD边上,连接BF.
(1)求△DEF的周长;
(2)求sin∠BFE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的曲边三角形可按下述方法作出:作等边三角形![]() ;分别以点
;分别以点![]() ,
,![]() ,
,![]() 为圆心,以
为圆心,以![]() 的长为半径作
的长为半径作![]() ,
,![]() ,
,![]() .三段弧所围成的图形就是一个曲边三角形,如果一个曲边三角形的周长为
.三段弧所围成的图形就是一个曲边三角形,如果一个曲边三角形的周长为![]() ,那么这个曲边三角形的面积是___________.
,那么这个曲边三角形的面积是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
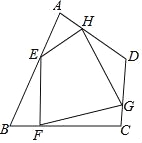
A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形
B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形
C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形
D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图.
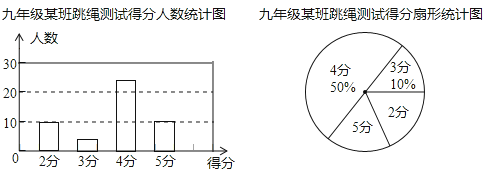
根据统计图解答下列问题:
(1)本次测试的学生中,得4分的学生有多少人?
(2)本次测试的平均分是多少分?
(3)通过一段时间的训练,体育组对该班学生的跳绳项目进行了第二次测试,测得成绩的最低分为3分.且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得4分、5分的学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
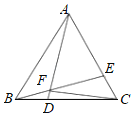
【题目】如图,在等边△ABC中,BD=CE,连接AD、BE交于点F.
(1)求∠AFE的度数;
(2)求证:ACDF=BDBF;
(3)连接FC,若CF⊥AD时,求证:BD=![]() DC.
DC.
查看答案和解析>>
科目:初中数学 来源: 题型:
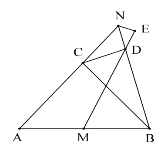
【题目】如图,△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,点 N 为射线 AC 上一点,连接 BN,过点 C 作 CD⊥BN 于点 D,连接 MD,作∠BNE=∠BNA,边 EN 交射线 MD 于点 E,若 AB=20![]() ,MD=14
,MD=14![]() ,则 NE 的长为___.
,则 NE 的长为___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com