
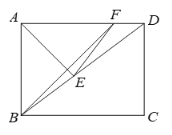
【题目】如图,在矩形ABCD中,AB=6,BC=8,点E是对角线BD上的一点,把△ABE沿着直线AE翻折得到△AFE,且点F恰好落在AD边上,连接BF.
(1)求△DEF的周长;
(2)求sin∠BFE的值.
【答案】(1)12;(2)![]()
【解析】
解法一:(1)首先根据矩形的性质和勾股定理得出BD的长度,然后由折叠的性质得出![]() ,则
,则![]() 的周长为
的周长为![]() ,代入相应的数值即可计算;
,代入相应的数值即可计算;
(2)作![]() 于点
于点![]() ,首先由
,首先由![]() 得出
得出![]() ,然后利用
,然后利用![]() 求出FG的长度,利用勾股定理求出BF的长度,则
求出FG的长度,利用勾股定理求出BF的长度,则![]() ,则答案可求;
,则答案可求;
解法二:(1)首先根据矩形的性质和勾股定理得出BD的长度,然后由折叠的性质得出![]() ,则
,则![]() 的周长为
的周长为![]() ,代入相应的数值即可计算;
,代入相应的数值即可计算;
(2)延长![]() 交
交![]() 于点
于点![]() ,首先轴对称性质可得
,首先轴对称性质可得![]() ,进而得出
,进而得出![]() 为等腰直角三角形,然后利用
为等腰直角三角形,然后利用![]() 得出
得出![]() ,进而求出BE,EF的长度,然后利用勾股定理求出BF的长度,进而求出FN的长度,再利用勾股定理求出EN的长度,最后利用
,进而求出BE,EF的长度,然后利用勾股定理求出BF的长度,进而求出FN的长度,再利用勾股定理求出EN的长度,最后利用![]() 即可求解.
即可求解.
解法一: ![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() .
.
在![]() 中,
中,![]() ,
,
由勾股定理得![]() .
.
由轴对称性质可得![]() ,
,
![]() ,
,
![]() 的周长
的周长![]() ;
;
![]() 作
作![]() 于点
于点![]() ,
,
![]()
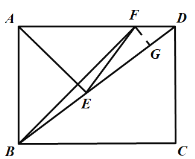
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
解得![]() .
.
在![]() 中,
中,![]() ,由勾股定理得
,由勾股定理得![]() .
.
在![]() 中,
中,
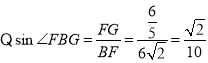 ,
,
![]() .
.
解法二:![]() 同解法一;
同解法一;
![]() 如图2,延长
如图2,延长![]() 交
交![]() 于点
于点![]() ,记
,记![]() 的交点为
的交点为![]() ,
,

由轴对称性质可得![]() ,
,
又![]() ,
,
![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() ,
,
![]()
![]() ,
,
![]() ,
,
即![]() ,
,
解得![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,
由勾股定理得![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,
由勾股定理得![]() ,
,
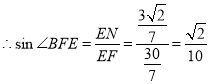 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校为调查“停课不停学”期间九年级学生平均每天上网课时长,随机抽取了![]() 名九年级学生做网络问卷调查.共四个选项:
名九年级学生做网络问卷调查.共四个选项:![]() 小时以下)、
小时以下)、![]() 小时)、
小时)、![]() 小时),
小时), ![]() 小时以上),每人只能选一
小时以上),每人只能选一
项.并将调查结果绘制成如下不完整的统计表和统计图.
被调查学生平均每天上网课时间统计表
时长 | 所占百分比 |
|
|
|
|
|
|
|
|
合计 |
|
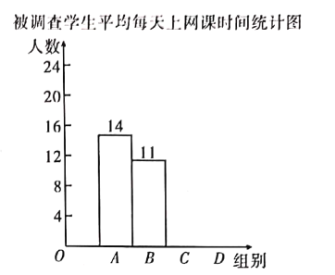
根据以上信息,解答下列问题:
![]() ,
,![]() ,
,
![]() 补全条形统计图;
补全条形统计图;
![]() 该校有九年级学生
该校有九年级学生![]() 名,请你估计仝校九年级学生平均每天上网课时长在
名,请你估计仝校九年级学生平均每天上网课时长在![]() 小时及以上的共多少名;
小时及以上的共多少名;
![]() 在被调查的对象中,平均每天观看时长超过
在被调查的对象中,平均每天观看时长超过![]() 小时的,有
小时的,有![]() 名来自九
名来自九![]() 班,
班,![]() 名来自九
名来自九![]() 班,其余都来自九
班,其余都来自九![]() 班,现教导处准备从
班,现教导处准备从![]() 选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的
选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的![]() 名学生恰好来自同一个班级的概率.
名学生恰好来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
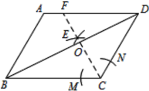
【题目】如图,在平行四边形ABCD中,AB=4,BC=5,∠ABC=60°. 按以下步骤作图:①以C为圆心,以适当长为半径做弧,交CB、CD于M、N两点;②分别以M、N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点E,作射线CE交BD于点O,交AD边于点F;则BO的长度为( )
MN的长为半径作弧,两弧相交于点E,作射线CE交BD于点O,交AD边于点F;则BO的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
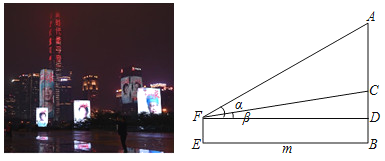
【题目】2020年3月20日,深圳市民中心及周边楼宇为当日返回深圳的援鄂医疗队员亮灯,欢迎最美逆行者回家.小洪在欢迎英雄回家现场,如图,若他观测到英雄画像电子屏顶端A和底端C的仰角分别为∠α和∠β,小洪所站位置E到电子屏边缘AC垂直地面的B点距离为m米,那么英雄画像电子屏高AC为( )
A.![]() 米B.mtan(α﹣β)米
米B.mtan(α﹣β)米
C.m(tanα﹣tanβ)米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
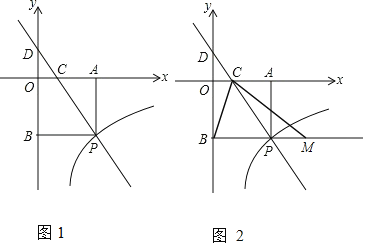
【题目】如图1,直线y1=kx+3与双曲线![]() (x>0)交于点P,PA⊥x轴于点A,PB⊥y轴于点B,直线y1=kx+3分别交x轴、y轴于点C和点D,且S△DBP=27,
(x>0)交于点P,PA⊥x轴于点A,PB⊥y轴于点B,直线y1=kx+3分别交x轴、y轴于点C和点D,且S△DBP=27,![]() .
.
(1)求OD和AP的长;
(2)求m的值;
(3)如图2,点M为直线BP上的一个动点,连接CB、CM,当△BCM为等腰三角形时,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5μm(0.0000025m)的颗粒物,含有大量有毒、有害物质,也称可入肺颗粒物.将0.0000025用科学记数法表示为
A.25×10﹣7B.2.5×10﹣6C.0.25×10﹣5D.2.5×106
查看答案和解析>>
科目:初中数学 来源: 题型:
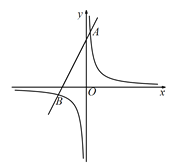
【题目】如图,在平面系中,一次函数![]() 的图像经过定点A,反比例函数
的图像经过定点A,反比例函数![]() 的图像经过点A,且与一次函数
的图像经过点A,且与一次函数![]() 的图像相交于点B(
的图像相交于点B(![]() ,m).
,m).
(1)求m、a的值;
(2)设横坐标为n的点P在反比例函数图象的第三象限上,且在点B右侧,连接AP、BP,△ABP的面积为12,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两张完全重合的矩形纸片,将其中一张绕点![]() 顺时针旋转
顺时针旋转![]() 后得到矩形
后得到矩形![]() (如图1),连接
(如图1),连接![]() ,
,![]() ,若
,若![]() ,
,![]() .
.

(1)试探究线段![]() 与线段
与线段![]() 的数量关系和位置关系,并说明理由;
的数量关系和位置关系,并说明理由;
(2)把![]() 与
与![]() 剪去,将
剪去,将![]() 绕点
绕点![]() 顺时针旋转得
顺时针旋转得![]() ,边
,边![]() 交
交![]() 于点
于点![]() (如图2),设旋转角为
(如图2),设旋转角为![]() ,当
,当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的度数;
的度数;
(3)若将![]() 沿
沿![]() 方向平移得到
方向平移得到![]() (如图3),
(如图3),![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 时,求平移的距离.
时,求平移的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com